7.2.1 Geschwindigkeitspolaren von Segelflugzeugen
Dieses Kapitel ist wie folgt gegliedert
- Allgemeines
- Geschwindigkeitspolare
- Sollfahrt – Gleitflugstrecke
- MacCready-Ring (MC-Ring) und Sollfahrtgeber
- Kreisflug und Reise mit Wasserballast
Allgemeines
In diesem Abschnitt geht es um zwei grundsätzliche Themen:
- Im Segelflugzeug fliegt man durch mal mehr, mal weniger stark absinkende Luftmassen. Für jedes Luftmassensinken gibt es abhängig von der jeweiligen Flächenbelastung des Segelflugzeugs eine optimale Geschwindigkeit, bei der für eine bestimmte Gleitflugstrecke möglichst wenig Höhe verbraucht wird bzw.
- wenn der nächste gute Aufwind sicher erreicht werden kann, dann lohnt es sich, schneller zu fliegen und somit früher in dem Aufwind anzukommen. Es geht also hier um die Frage, mit welcher Geschwindigkeit man zwischen zwei Aufwinden fliegen muss, um die Reisegeschwindigkeit zu optimieren.
 |
Geschwindigkeitspolare
Im Flughandbuch deines Segelflugzeugs findest du die zu diesem Flugzeug gehörende Geschwindig-keitspolare. Die Geschwindigkeitspolare unterscheidet sich von Segelflugzeugtyp zu Segelflugzeugtyp.
Das folgende Bild zeigt eine Kopie aus dem Flughandbuch einer LS 4a.
 Geschwindigkeitspolare einer LS 4a
Geschwindigkeitspolare einer LS 4a
Bei einer Geschwindigkeitspolare ist die Sinkgeschwindigkeit eines Segelflugzeugs in ruhender Luft als Kurve gegenüber der Fluggeschwindigkeit abgetragen. Die Polare im Flughandbuch bezieht sich auf ein sauberes Tragflügelprofil, also ohne Verschmutzungen z.B. durch Mücken auf der Profilnase.
Das obige Beispiel der LSx4a zeigt zwei verschiedene Kurven, eine für eine Flächenbelastung von 33xkg/m2 und eine für 50xkg/m2. Unter Flächenbelastung versteht man die Flugmasse (siehe Kapitel 7.1) des Segelflugzeugs geteilt durch die Flügelfläche. Eine LSx4a hat ca.10xm2 Flügelfläche. Bei einer Flächenbelastung von 33xkg/m2 beträgt die Flugmasse folglich 330xkg.
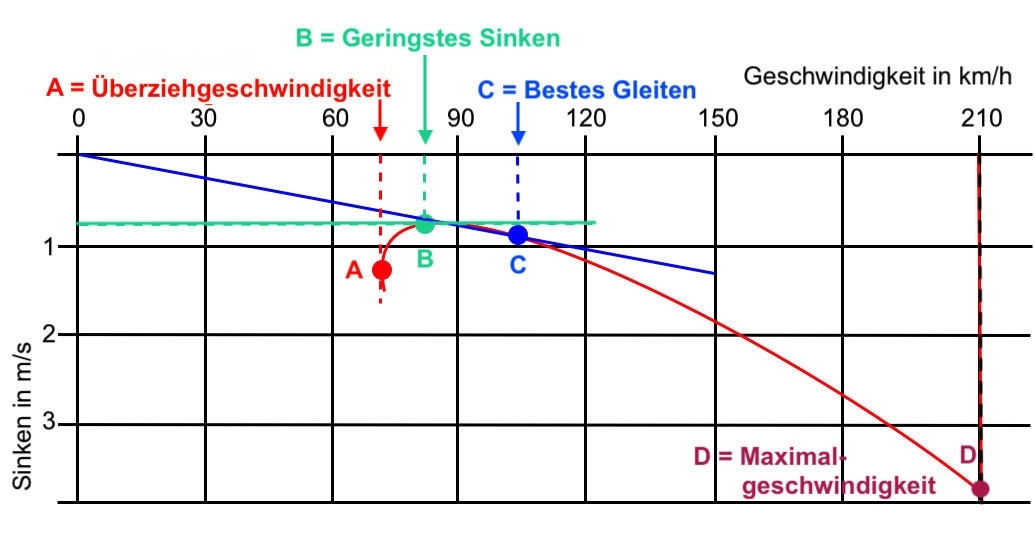
Zum besseren Verständnis beider Geschwindigkeitspolaren werden die folgenden vier charakteristischen Geschwindigkeiten betrachtet, die in der Abbildung unten mit A, B, C und D markiert sind (siehe auch Kapitel 5.2):
Überziehgeschwindigkeitx„A“: Bei Annäherung an die Überziehgeschwindigkeit beginnt das Segelflugzeug (mehr oder weniger stark) zu schütteln und die Strömung auf der Flügeloberseite beginnt, sich abzulösen und wird zunehmend turbulent.
Geschwindigkeit des geringsten Sinkens „B“: Dies ist der höchste Punkt auf der Polare. Bei dieser Geschwindigkeit kann man (in ruhiger Luft) am längsten fliegen, weil das Segelflugzeug hier die niedrigste Sinkgeschwindigkeit aufweist.
Geschwindigkeit des besten Gleitens „C“: Bei dieser Geschwindigkeit kann das Segelflugzeug aus einer bestimmten Höhe die größtmögliche Strecke zurücklegen. Das Verhältnis von Fluggeschwindigkeit zu Sinkgeschwindigkeit, die sogenannte Gleitzahl, wird dabei maximal und es wird der beste (= kleinste) Gleitwinkel erzielt.
ZulässigexHöchstgeschwindigkeitx(VNE)x„D“: Die zulässige Höchstgeschwindigkeit wird vom Hersteller des Segelflugzeugs auf Basis von Festigkeitsberechnungen für den Tragflügel festgesetzt.
(Anmerkung: Die in Flughandbüchern veröffentlichen Geschwindigkeitspolaren sind nicht immer bis zu dieser Höchstgeschwindigkeit gezeichnet).
Sollfahrt - Gleitflugstrecke
Geschwindigkeit des besten Gleitens
Um sich mit den Flugleistungen des Segelflugzeugs, mit dem du Überlandfliegen willst, vertraut zu machen, ist es sinnvoll, sich die Polare aus dem Flughandbuch herauszukopieren und zu studieren. Unten ist die Geschwindigkeitspolare einer ASW 28 mit 15 m Spannweite abgebildet. Zu sehen sind die Polare für eine Flächenbelastung von 31 kg/m2 und die Polare für eine Flächenbelastung von 50 kg/m2.
Bei einer Flächenbelastung von 31 kg/m2 beträgt die Geschwindigkeit des besten Gleitens 92 km/h und bei einer Flächenbelastung von 50 kg/m2 sind es 115 km/h.
 Geschwindigkeitspolare mit bestem Gleiten
Geschwindigkeitspolare mit bestem Gleiten
Die ASW 28 hat eine maximale Gleitzahl von 45. Aus 1000 m Höhe kann das Segelflugzeug theoretisch 45 km weit fliegen. Der Wert gilt für ein Flugzeug mit abgeklebten Flächen und ohne Verschmutzung der Flügel. Anhand der beiden gezeigten Polaren für unterschiedliche Flächenbelastungen sieht man, dass sich die Polare bei einer höheren Flächenbelastung nach rechts und leicht nach unten verschiebt. Die Geschwindigkeit des besten Gleitens nimmt mit höherer Flächenbelastung also zu und die zugehörige Sinkgeschwindigkeit wird ebenfalls höher, aber die maximale Gleitzahl bleibt (in etwa) gleich.
Weiter unten siehst du die Geschwindigkeitspolare aus dem Flughandbuch der DG-300.
Dem Handbuch kannst du die folgenden Daten entnehmen:
| Flächenbelastung W/S | 32 kg/m² | 40 kg/m² | 50 kg/m² |
| Überziehgeschwindigkeit | 68 km/h | 77 km/h | 86 km/h |
| Geringstes Sinken | 0,56 m/s | 0,62 m/s | 0,68 m/s |
| bei | 78 km/h | 87 km/h | 98 km/h |
| Gleitzahl | 41 | 41,5 | 42 |
| bei | 100 km/h | 112 km/h | 122 km/h |
Geschwindigkeit und Flächenbelastung
Man erkennt, dass bei einer höheren Flächenbelastung sowohl die Überziehgeschwindigkeit als auch die Geschwindigkeit des geringsten Sinkens und die Geschwindigkeit des besten Gleitens grösser werden.
Maximale Gleitzahl und Geschwindigkeit des besten Gleitens
Ebenso sieht man, dass bei einer höheren Flächenbelastung die maximale Gleitzahl (fast) unverändert bleibt, allerdings wird bei der höheren Flugmasse (= höhere Flächenbelastung) die beste Gleitzahl bei einer höheren Geschwindigkeit erreicht.
Bei der DG-300 wird die maximale Gleitzahl bei höheren Flächenbelastungen sogar noch etwas grösser. Bei einer Flächenbelastung von 50 kg/m2 wird die maximale Gleitzahl bei einer Fluggeschwindigkeit von 122xkm/h erreicht. Die Sinkgeschwindigkeit ist dann 0,807 m/s und die zugehörige Gleitzahl 42, verglichen mit 41 bei 32 kg/m2.
Kräftegleichgewicht zwischen Auftrieb und Gewichtskraft am Segelflugzeug
Die Größe des Auftriebs hängt von der Fluggeschwindigkeit und dem Anstellwinkel ab. Im (unbe-schleunigten) Gleitflug sind Auftrieb L und Gewichtskraft G betragsmäßig ungefähr gleich groß.
Korrekt ausgedrückt ist die nach unten wirkende Gewichtskraft G im Gleichgewicht mit der entgegengesetzt wirkenden resultierenden Luftkraft R
Im obigen Bild sieht man, dass die Auftriebskraft L genau senkrecht zur Anströmrichtung wirkt. Der Widerstand W wirkt parallel zur Anströmung entgegen der Flugrichtung. Die Vektorsumme dieser beiden Kräfte, also das Addieren der beiden Pfeile ergibt die resultierende Luftkraft R, die genau entgegengesetzt der Gewichtskraft G wirkt.
Bei einem Segelflugzeug ist der Winkel zwischen dem Auftrieb L und der resultierenden Luftkraft R beim Geradeausflug im normalen Geschwindigkeitsbereich sehr klein, d.h. die beiden Pfeile für L und R sind nahezu gleich lang bzw. die beiden Kräfte annähernd gleich groß.
Eine ausführlichere Erklärung zur Kräftebilanz am Segelflugzeug findet sich in Kapitel 5.1 - Aerodynamik: Anstellwinkel, Geschwindigkeit und Flugmasse.
Bei der Geschwindigkeit des besten Gleitens fliegst du mit dem optimalen Verhältnis zwischen Fluggeschwindigkeit und Eigensinken des Segelflugzeugs.
Für die DG-300 (W/S 32 kg/m2) sind die entsprechenden Werte 100 km/h Fluggeschwindigkeit und 0,67xm/s Eigensinken. Die zugehörige Gleitzahl erhält man, indem man die beiden Geschwindigkeiten auf die gleiche Einheit umrechnet, also entweder m/s oder km/h und dann den Betrag der Fluggeschwindigkeit durch den Betrag der Sinkgeschwindigkeit teilt. Im obigen Beispiel und mit der Einheit m/s ergibt das 27,7x/x0,67x»x41,45. Die beste Gleitzahl der DG-300 mit W/S 32xkg/m2 beträgt also ca. 41.
Den zugehörigen Gleitwinkel kann man ebenfalls ausrechnen: Die Skizze unten zeigt, dass der Tangens des Gleitwinkels E dem Kehrwert der Gleitzahl entspricht, im Beispiel also tan E = 1/41 = 0,0243. Das ergibt einen Gleitwinkel von ca. 1,4°, d.h. die Flugbahn ist bei dieser Geschwindigkeit gegenüber der Horizontalen um 1,4° nach unten geneigt.

Gleitwinkel
Was geschieht, wenn du jetzt mit der Geschwindigkeit des geringsten Sinkens fliegen willst? Dazu musst du die Längsneigung des Flugzeugs verringern (Flugzeugnase bewegt sich nach oben), damit erhöht sich der Anstellwinkel und die Geschwindigkeit geht zurück. In der Folge stellt sich ein neues Gleichgewicht zwischen Gewichtskraft und Auftrieb (bzw. resultierender Luftkraft R) ein. Du fliegst jetzt mit der Geschwindigkeit des geringsten Sinkens, bei der DG-300 (WS 32 kg/m2) entspricht das 78 km/h bei 0,56xm/s Sinkgeschwindigkeit.
Die Gleitzahl verschlechtert sich dabei von 41 auf 38, d.h. man kann bei dieser Geschwindigkeit aus gleicher Höhe nicht mehr so weit gleiten, bleibt dafür aber länger in der Luft.
Was ändert sich, wenn man die DG-300 mit und ohne Wasserballast jeweils z.B. mit 100 km/h fliegt?
- Wenn du ohne Wasserballast in ruhiger Luft mit 100 km/h fliegst, fliegst du mit dem besten Gleitwinkel, also dem optimalen Verhältnis zwischen Fluggeschwindigkeit und Eigensinken für diese Flächenbelastung.
- Wenn du mit Wasserballast (also mit einer höheren Flugmasse bzw. Flächenbelastung) und ebenfalls mit 100 km/h fliegst, brauchst du im Vergleich zum Beispiel ohne Wasserballast einen größeren Anstellwinkel, um die erhöhte Gewichtskraft durch den Auftrieb auszugleichen. Dabei erzielst du nicht mehr den optimalen Gleitwinkel, die Gleitzahl beträgt jetzt noch 37.
Fazit: Für jede Flächenbelastung gibt es eine bestimmte Geschwindigkeit für geringstes Sinken und eine für den besten Gleitwinkel (bzw. die maximale Gleitzahl).
Bestimmen der Geschwindigkeit für den besten Gleitwinkel
Du ermittelst die Geschwindigkeit für den besten Gleitwinkel (die maximale Gleitzahl), indem du vom Ursprung des Koordinatensystems aus, eine Tangente an die Polare legst. Dort, wo die Tangente die Polare berührt, ziehst du eine senkrechte Line nach oben, um auf der Geschwindigkeitsachse die zugehörige Geschwindigkeit abzulesen.
Im Bild erkennt man, dass diese Geschwindigkeit für die LS 4 ohne Wasserballast und in ruhiger Luft ca.x95xkm/hxbeträgt.
 Polare und bestes Gleiten LS 4 ohne Wasserballast (32,8 kg/m2)
Polare und bestes Gleiten LS 4 ohne Wasserballast (32,8 kg/m2)
Ermitteln der Geschwindigkeit für den besten Gleitwinkel beim Durchfliegen eines Abwindgebiets
Wenn du durch Abwinde fliegst, verschiebt sich die Polare um den Betrag der Sinkgeschwindigkeit des Abwinds nach unten. Wenn du jetzt eine Tangente vom Ursprung an die verschobene Polare legst, erhältst du eine höhere Geschwindigkeit für den besten Gleitwinkel und der Gleitwinkel bzw. die Gleitzahl verschlechtern sich.
 Polare und bestes Gleiten im Abwindgebiet mit 1 m/s Sinken
Polare und bestes Gleiten im Abwindgebiet mit 1 m/s Sinken
MacCready-Ring und Sollfahrtgeber
Viele Segelflugzeuge haben einen MacCready-Ring (MC-Ring) am Variometer, einen Sollfahrtgeber und einen Endanflugrechner (oder einen Bordcomputer mit einem Modul für die Endanflugberechnung).
Der MC-Ring und der Sollfahrtgeber sollen dabei helfen, Strecken durch Sink- und Steigwindgebiete mit der optimalen Vorfluggeschwindigkeit zurückzulegen oder mit der Geschwindigkeit für den besten Gleitwinkel zurück zum Platz zu fliegen.
Mit dem Endanflugrechner werden die erforderliche Höhe und die Geschwindigkeit ermittelt, um optimal (=xso schnell wie möglich) aus dem letzten Aufwind zum Heimatflugplatz zu fliegen.
 MacCready-Ring MacCready-Ring |
Mit dem MC-Ring bestimmt man die optimale Vorfluggeschwindigkeit, wenn man ohne Wasser-ballast fliegt. Mit dem Sollfahrtgeber (oft kombiniert mit einem akustischen Variometer) und dem Endanflugrechner ist es möglich, die Anzeigen an unterschiedliche Flächenbelastungen (also mit Wasserballast) anzupassen. Denk daran, dass die (angezeigte) Sollfahrt bei einem stark verschmutzten Flügel nicht mehr stimmt und schon gar nicht beim Fliegen im Regen.
|
Bei Flügen durch Regenschauer verschlechtern sich die aerodynamischen Eigenschaften des Flugzeugs infolge der nassen Tragflächen und die Überziehgeschwindigkeit kann sich dadurch deutlich erhöhen. Zusätzlich tritt im Regen oft auch verstärktes Luftmassensinken auf. Wenn du im Regen fliegst, solltest du daher deutlich schneller als mit der angezeigten Sollfahrt fliegen. Das Flughandbuch deines Flugzeuges enthält gegebenenfalls weitere Hinweise zum Fliegen in Regen.
Beste Geschwindigkeit für Abwindgebiete
Wenn du zum Platz zurückfliegst, wirst du durch Bereiche mit Abwinden und Bereiche mit Aufwinden fliegen. Um bei vernachlässigbarem Wind möglichst hoch am Platz anzukommen, fliegst du mit Hilfe des MacCready-Rings. Auf dem drehbaren Ring (der außen um die Variometeranzeige herum angebracht ist) siehst du einen Pfeil bzw. ein Dreieck. Dieser Pfeil sollte auf 0 m/s stehen. Bei Durchfliegen von Abwinden zeigt die Nadel des Variometers auf die Fluggeschwindigkeit des besten Gleitens für die aktuelle Sinkgeschwindigkeit. Diese Geschwindigkeit hältst du grob ein. Wenn das Variometer ein Sinken von 2,5xm/s anzeigt, solltest du nach dem MC-Ring in der Abbildung etwa 120 km/h fliegen.
Gegen den Wind zum Platz zurückfliegen
Wenn du gegen den Wind fliegst und den Platz oder Zielpunkt möglichst hoch erreichen willst, musst du schneller fliegen als bei Windstille. Um wieviel schneller man fliegen muss, ergibt sich aus der Geschwindigkeitspolare.
Wenn du z.B. bei 35 km/h Gegenwind fliegst, musst du die Polare um den Betrag der Windgeschwindigkeit nach links verschieben. Weil das nicht sonderlich praktikabel ist, verschiebst du stattdessen den Ursprung des Koordinatensystems um den Betrag der Windgeschwindigkeit nach rechts.
Im vorliegenden Beispiel musst du die Tangente also vom Punkt 35 km/h auf Geschwindigkeitsachse aus an die Polare anlegen.
Die zugehörige Geschwindigkeit des besten Gleitens ergibt sich dabei zu ca. 105 km/h. Wenn man die Tangente nach links verlängert, bis sie die senkrechte Achse des Koordinatensystems schneidet, liest man für die LS 4 einen Wert von +0,4 m/s ab. Wenn du also bei einem Gegenwind von 35 km/h den MC-Ring auf +0,4 m/s stellst, bekommst du damit die Geschwindigkeit des besten Gleitens, mit der du bei diesem Gegenwind möglichst hoch am Platz ankommst.
Man muss dabei aber beachten, dass die Gleitzahl gegenüber Windstille deutlich reduziert ist. Wenn man bei 35 km/h Gegenwindkomponente mit Fahrtmesseranzeige 105 km/h fliegt, hat man gegenüber dem Boden nur eine Geschwindigkeit von 70 km/h bei einem Eigensinken von knapp 0,8 m/s. Die Gleitzahl gegenüber dem Boden beträgt in diesem Fall also nur ca. 24.
Da du beim Fliegen meist nicht genau weißt, wie stark der Gegenwind ist, kannst du die MC-Einstellung wie folgt abschätzen: Bei mäßigem Gegenwind stellst du den Ring auf +0,25 m/s ein und bei kräftigem Gegenwind auf +0,5 m/s.
| Gegenwind | Stärke |
Ringeinstellung |
| moderat | 5 m/s = 10 Knoten = 18 km/h | + 0.25 m/s |
| kräftig | 10 m/s = 20 Knoten = 36 km/h | + 0.5 m/s |
| stark | 15 m/s = 30 Knoten = 54 km/h | + 0.75 m/s |
Sollfahrtgeber
Anstatt den Ring auf z.B. plus 1 m/s zu drehen, kannst du den Sollfahrtgeber mit der MC-Taste auf eine beliebige Steiggeschwindigkeit einstellen. Wenn der Zeiger höher als 0 m/s anzeigt, fliegst du zu schnell. Nimm die Fahrt zurück, dann geht die Anzeige entsprechend zurück. Wenn der Sollfahrtgeber weniger als 0xm/s anzeigt, musst du die Fahrt erhöhen.
Kreisflug und Reise mit Wasserballast
- Lies vor dem Fliegen mit Wasserballast die entsprechenden Seiten im Flughandbuch;
- das Fliegen mit Wasserballast lohnt sich nur bei Aufwinden mit großem Durchmesser und guten Steigwerten;
- vor der Landung muss der Wasserballast abgelassen werden.
Auf den ersten Blick mag es seltsam erscheinen, aber unter bestimmten Bedingungen verbessern sich die Flugleistungen mit einer höheren Flugmasse. Für die gleiche Gleitzahl kann man mit Wasserballast schneller fliegen als ohne. Das weiter unten abgebildete Diagramm mit Polaren für 2 verschiedenen Flächenbelastungen zeigt, dass du bei diesem Flugzeug beim Fliegen mit Wasserballast (45 kg/m2) bei ca. 160 km/h das gleiche Sinken hast wie bei einer Geschwindigkeit von 145 km/h ohne Wasserballast (32,2xkg/m2). Die Vorfluggeschwindigkeit mit Wasserballast ist höher und das ergibt (bei guter Thermik) eine höhere Reisegeschwindigkeit. Die höhere Flächenbelastung wird durch das Mitführen von Wasserballst in speziell dafür vorgesehenen Wassertanks oder Wassersäcken in den Tragflächen erreicht. Bevor du einen neuen Flugzeugtyp mit Wasserballast fliegst, solltest du vorher immer im Flughandbuch nachlesen, was es dabei zu beachten gibt. Man findet dort nicht nur die Geschwindigkeitspolaren für das Fliegen mit und ohne Wasserballast, sondern auch Angaben über die maximal zulässige Abflugmasse, die Verteilung des Wasserballasts in den Tragflächen und im Hecktank (soweit vorhanden) in Abhängigkeit von der Zuladung im Cockpit, die Überziehgeschwindigkeit usw.
Wegen der höheren Flugmasse mit Wasserballast muss auch der Auftrieb grösser werden, d.h. du musst mit einer höheren Geschwindigkeit fliegen.
 Bestes Gleiten bei höherer Flächenbelastung
Bestes Gleiten bei höherer Flächenbelastung
(Die eingezeichnete Zunahme der Reisegeschwindigkeit stimmt strenggenommen nur für den Fall Luftmassensinken 0 m/s und Steigen von +2xm/s)
Aus dem Polarendiagramm ist ersichtlich, dass mit Wasserballast:
- die Überziehgeschwindigkeit steigt;
- im niedrigen Geschwindigkeitsbereich das Eigensinken grösser ist als ohne Wasserballast;
- bei höheren Geschwindigkeiten das Eigensinken geringer ist als ohne Wasserballast;
- bei gleichen Steigwerten und Fliegen nach Sollfahrt ein besserer Gleitwinkel und eine höhere Reisegeschwindigkeit erzielt werden.
Anders ausgedrückt:
Man steigt mit Wasserballast schlechter, kann dafür aber schneller vorfliegen. Daraus ergibt sich ein Vorteil bei guter Thermik, weil der Nachteil des schlechteren Steigens durch den Vorteil des besseren Gleitens bei höherer Geschwindigkeit überkompensiert wird. Durch die höhere Reisegeschwindigkeit kann man ggf. insgesamt weitere Strecken zurücklegen.
In schwacher bis mäßiger Thermik fliegt man dagegen mit einem niedrigen MC-Wert und damit in einem entsprechend niedrigen Geschwindigkeitsbereich. Wenn man dann zusätzlich Wasser mitnimmt, steigt man noch schlechter. In diesem Fall verschlechtert sich die Flugleistung durch den Wasserballast.
Der Durchmesser der Aufwinde spielt ebenfalls eine Rolle dabei, ob es sinnvoll ist, Wasserballast mitzuführen, oder ob der Ballast abgelassen werden sollte. Für jeden Aufwind gibt es eine optimale Fluggeschwindigkeit mit der dazugehörigen Querneigung. Diese Parameter müssen dem jeweiligen Durchmesser des Aufwinds angepasst werden.
| Fluggeschwindigkeit und Kreisradius |
Zwei Segelflugzeuge im Kreisflug mit jeweils 45° Querneigung. Eines der Flugzeuge fliegt mit und eines ohne Wasserballast.
Das innen fliegende Flugzeug ohne Wasserballast fliegt mit 90 km/h bei einem Eigensinken von 1,2 m/s. Sein Kreisradius beträgt 62 m.
Das äußere Flugzeug mit Wasserballast fliegt mit 110 km/h bei einem Eigensinken von 1,4 m/s. Der Kreisradius ist dabei 93 m. |
Dem Bild kannst du entnehmen, dass bei großen Aufwinddurchmessern und normaler Querneigung das Eigensinken mit Wasserballast kaum größer ist als ohne Wasserballast (im Beispiel 0,2 m/s), aber der Kreisdurchmesser ist grösser. Bei schwacher Thermik, aber großflächigen Aufwinden ist die Mitnahme von Wasserballast daher immer noch vorteilhaft.
Viel nachteiliger ist die Wasserballastmitnahme bei engen Aufwinden, bei denen man entweder sehr steil kreisen muss oder mit einem großen Kreisdurchmesser weit außen im Aufwind fliegt, wo es kaum noch Steigen gibt.
Die Mitnahme von Wasserballast lohnt sich besonders an Tagen mit einem hohen und schnellen Geradeausfluganteil, was häufig bei Wetterlagen mit Wolkenstraßen der Fall ist. Der Nachteil ist, durch einen größeren Kreisradius beim Kurbeln reduziert sich das Steigen.
Ablassen von Wasserballast
Eine höhere Masse eines Flugzeugs erhöht die Belastung der Luftfahrzeugstruktur bei Flugmanövern und bei der Landung. Vermeide deshalb steiles Hochziehen und lasse den Wasserballast vor der Landung ab. Dabei ist zu beachten, dass es bis zu fünf Minuten dauern kann, bis das Wasser vollständig abgelassen ist. Wenn du dich bei schwacher Thermik dazu entschließt, den Wasserballast abzulassen, solltest du dich zuerst vergewissern, dass sich keine anderen Luftfahrzeuge unter dir befinden.
(mit freundlicher Genehmigung Tobias Barth Photographie)
Bei nachlassender Thermik kann der Wasserballast auch unterwegs abgelassen werden und es ist auch möglich, nur einen Teil des Wasserballasts abzulassen, wenn die Steigwerte nicht mehr gut genug für die maximale Flächenbelastung sind. Dazu musst du aber ungefähr wissen, wieviel Wasser pro Zeiteinheit abfließt.
Wenn dir während des Flugs Zweifel kommen, ob Wasserballast noch sinnvoll ist, handle nach dem Grundsatz: Im Zweifelsfall das Wasser ablassen.
Anker: Geschwindigkeitspolare = Gesch-1; Sollfahrt = Gesch-2; Mc-Ready = Gesch-3; Kreislfug = Gesch-4
xxxx