5.1.1 Grundlagen

Basics concepts, laws and definitions

Luft ist ein Gemisch von Gasen. Ruhende Luft besteht aus sehr vielen Molekülen, die sich kreuz und quer bewegen, jedes mit seiner eigenen Geschwindigkeit und Richtung.

5.1.1.1 Bewegung der Luftmoleküle

Wenn die Luftmoleküle mit der Oberfläche eines Gegenstands oder miteinander kollidieren, ändern sie ihre Richtung. Die Stöße dieser unzähligen Moleküle gegen die Oberfläche verursachen eine bestimmte Kraft auf eine festgelegte Fläche der Wand dieses Gegenstands, z.B. einen Quadratzentimeter. Die Kraft, die so auf eine Flächeneinheit wirkt (z.B. auf besagten Quadratzentimeter) ist der Luftdruck. Hieraus geht hervor, dass der Luftdruck immer gegen eine Wand wirkt, nie an ihr „zieht“. Auch auf die Oberseite eines Flügels drückt der Luftdruck, nur eben in geringerem Maße als auf die Unterseite.

Wenn trotzdem von „Unterdruck“ oder gar von „Sog“ die Rede ist, kommt das daher, dass man sich dann auf den herrschenden Normaldruck bezieht. Verglichen mit diesem kann der örtliche Druck größer sein (Überdruck) oder kleiner (Unterdruck). Der absolute Druck ist aber immer positiv.

Der Druck wird mit dem Buchstaben p bezeichnet, seine Einheit ist 1 Pascal (1 Pa = 1N/m²).

Der Luftdruck in der Atmosphäre ändert sich ständig und hängt unter anderem von der Höhe über dem Meeresspiegel ab.

Der durchschnittliche Luftdruck auf Meereshöhe (besser gesagt der Standardluftdruck) beträgt 1013,25 Hektopascal (hPa).

5.1.1.1 Luftdichte

Density

Die Luftdichte ist die Masse der Luft pro Volumeneinheit. Sie wird mit dem griechischen Buchstaben ρ (rho) bezeichnet. In der Standardatmosphäre beträgt die Luftdichte in Meereshöhe ρ₀ = 1,225 kg/m³. Das bedeutet, dass auf Meereshöhe 1 m³ Luft eine Masse von 1,225 kg hat.

Die Dichte der Luft nimmt mit der Höhe ab. In 2000 m Höhe beispielsweise ist sie auf 1,01 kg/m³ gesunken.

Dies liegt daran, dass sich in größeren Höhen weniger Luft oberhalb befindet, die Luft in der Höhe also mit weniger Kraft komprimiert wird. In einem Kubikmeter Luft befinden sich dann weniger Luftmoleküle, entsprechend geringer ist die Masse in einem Kubikmeter. Damit ist auch klar, dass die Luftdichte den Luftdruck beeinflusst, denn wie in Abb. 5.1.1.1.1 (Luftsäule) dargestellt, entsteht der Luftdruck durch das Gewicht einer Luftsäule mit 1 m² Querschnitt oberhalb der Messstelle.

Abb. 5.1.1.1.1 Luftsäule

Den Wert von 1,225 kg/m³ für die Luftdichte in Meereshöhe solltest du dir merken!

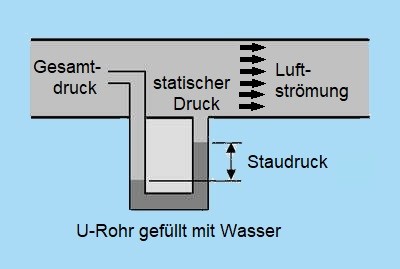
5.1.1.2 Statischer Druck, Staudruck und Gesamtdruck

Static pressure, dynamic pressure and total pressure

Wenn du im Flug die Hand aus dem Schiebefenster hältst, spürst du die Anströmung. Die Kraft kommt vom Luftdruck, aber die Ursache liegt in der zusätzlichen, gerichteten Bewegung der strömenden Luftmoleküle. Wir müssen also unterscheiden:

Wenn die Luft stillsteht, bewegen sich die Moleküle zufällig hin und her und verursachen dadurch einen bestimmten Druck. Diesen Druck, dessen Größe in erster Linie die Schwerkraft bestimmt (siehe Abb. 5.1.1.1 Bewegung der Luftteilchen), nennen wir den statischen Druck.

Wenn der Fahrtwind auf das Flugzeug trifft, oder – was das Gleiche ist – wenn sich das Flugzeug mit einer entsprechenden Geschwindigkeit durch die Luft bewegt, dann kommt zu dieser Hin- und Herbewegung die Strömungsgeschwindigkeit. Den durch die Strömungsbewegung verursachten Druck nennen wir den dynamischen Druck oder den Staudruck.

Die Summe aus beiden Drücken, also aus statischem Druck und Staudruck, ist der Gesamtdruck.

Wenn du Drücke messen willst, musst du auf die Richtung der Messöffnung achten.

Nur in ruhender Luft ist die Messrichtung egal, du misst immer den statischen Druck.
Bei strömender Luft muss die Messöffnung quer zur Strömungsrichtung orientiert sein, damit du den statischen Druck messen kannst.
Wenn die Messöffnung in Strömungsrichtung orientiert ist, erhältst du die Summe aus statischem Druck und Staudruck, nämlich den Gesamtdruck.

Das heißt, du musst vom gemessenen Gesamtdruck den statischen Druck abziehen, um den Staudruck zu erhalten. Direkt messen lässt er sich nicht.

Die folgende Abbildung zeigt eine Messanordnung, mit der die Druckdifferenz anzeigt werden kann.

Abb. 5.1.1.2.1 Messung des Staudrucks

Den Staudruck bezeichnet man mit q. Er steigt mit zunehmender Luftdichte ρ und mit der Anströmgeschwindigkeit V, wobei die Geschwindigkeit einen größeren Einfluss hat. Dies drückt sich dadurch aus, dass in der Formel für den Staudruck die Geschwindigkeit im Quadrat steht:

Wenn sich also die Geschwindigkeit verdoppelt, wird der Staudruck viermal so groß. Der Faktor ½ hat keine besondere Bedeutung, er ergibt sich aus der Mathematik, wenn man die Formel herleitet.

5.1.1.3 Wahre und angezeigte Geschwindigkeit

IAS und TAS

Die in Abb. 5.1.1.4.1 (Strömung bei Querschnittsänderung, Button drücken) dargestellte Messanordnung wird für die Fahrtmesseranzeige benutzt. Der Fahrtmesser entspricht dem U-Rohr.

Die Formel für den Staudruck stellen wir so um, dass wir die Geschwindigkeit erhalten:

Der Staudruck q ist also ein Maß für die Geschwindigkeit. Wie die Formel gerätetechnisch umgesetzt wird, lernst du im Fach Allgemeine Luftfahrzeugkunde. Allerdings wird dabei die Luftdichte ρ nicht einbezogen, obwohl sie auch in der Formel steht. Es wäre zwar denkbar, ihren Einfluss auf die Geschwindigkeitsanzeige im Fahrtmesser zu berücksichtigen, aber es gibt gute Gründe, dies nicht zu tun.

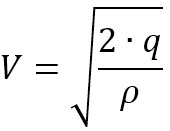
Deswegen müssen wir akzeptieren, dass die auf dem Fahrtmesser abzulesende Geschwindigkeit nicht die tatsächliche Geschwindigkeit ist. Wir unterscheiden:

Die angezeigte Geschwindigkeit (indicated airspeed IAS) ist die Geschwindigkeit, die ein Staudruck-Fahrtmesser anzeigt, der für Normalatmosphäre/Höhe Null geeicht ist.

Die wahre Geschwindigkeit (true airspeed TAS) ist die Geschwindigkeit eines Luftfahrzeugs in ruhender Luft.

IAS und TAS sind nur in Meereshöhe gleich, und auch nur bei den Bedingungen der Normalatmosphäre und wenn es keine Gerätefehler oder Einbaufehler gibt. Wenn die Luftdichte mit zunehmender Flughöhe immer kleiner wird, zeigt der Fahrtmesser eine zu geringe Geschwindigkeit an. Was das bedeutet und welche Folgen das hat, lernst du später.

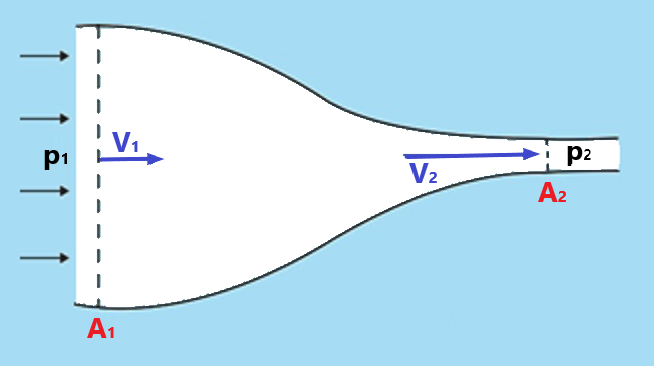
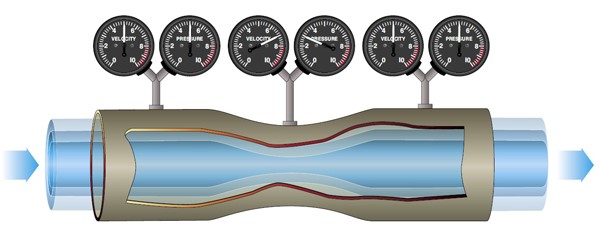
5.1.1.4 Kontinuitätsgesetz

Continuity law

Nach dem Kontinuitätsgesetz bleibt der Massenstrom konstant, wenn die Luft durch ein (reales oder imaginäres) Rohr strömt. Unter Massenstrom verstehen wir, welche Luftmenge (in kg) sich pro Sekunde durch einen Querschnitt bewegt. Der Massenstrom, der in das Rohr eintritt, ist der gleiche wie der Massenstrom, der austritt.

Wenn bei kleiner werdendem Durchmesser die gleiche Luftmenge durch das Rohr strömt, muss die Geschwindigkeit der Luft zunehmen. Wird der Rohrdurchmesser größer, muss die Geschwindigkeit abnehmen. Wenn der Querschnitt des Rohres halb so klein ist, wird die Geschwindigkeit doppelt so groß. Dabei wird vorausgesetzt, dass die Luft nicht kompressibel ist. Bei Geschwindigkeiten bis zu 250 km/h stimmt diese Annahme sehr gut.

Abb. 5.1.1.4.1 Strömung bei Querschnittsänderung

p₁ ist der Luftdruck bei Eintritt in das Rohr. Es hat hier den Querschnitt A₁, die Geschwindigkeit ist V₁. Nach rechts verjüngt sich der Querschnitt auf A₂, die Geschwindigkeit der Luft steigt auf V₂ und der Luftdruck sinkt auf p₂. Das Kontinuitätsgesetz stellt die Beziehung zwischen Fließquerschnitt und Geschwindigkeit her:

5.1.1.5 Gesetz von Bernoulli

Bernoulli's equation

Daniel Bernoulli (1700 – 1782) war ein Schweizer Mathematiker und Physiker. Bedeutsam für die Strömungslehre ist ein nach ihm benanntes Gesetz. Dieses beruht auf dem Energieerhaltungssatz, nach dem sich „die Gesamtenergie eines abgeschlossenen Systems mit der Zeit nicht ändert“.

Allerdings kann innerhalb des abgeschlossenen Systems Energie zwischen den verschiedenen Energieformen umgewandelt werden. Solche Energieformen sind z.B. chemische, thermischen, elektrische oder auch Kernenergie.

Das Gesetz von Bernoulli bezieht sich auf mechanische Energieformen von Gasen, nämlich Druckenergie und kinetische Energie. Es lautet:

Gesamtdruck = statischer Druck + Staudruck = konstant

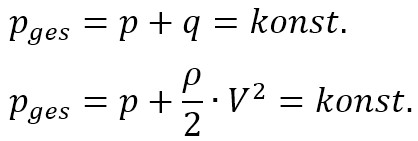
Im statischen Druck steckt die Druckenergie, im Staudruck die Bewegungsenergie der Luftmoleküle. Wir nennen den Staudruck daher auch den dynamischen Druck.

Der Vollständigkeit halber sei noch gesagt, dass hier die potenzielle Energie (Energie der Lage) unberücksichtigt bleibt, weil ihr Einfluss verschwindend gering ist, und dass das Gesetz genau genommen auf einer Stromlinie gilt.

Wenn du dir die Bernoulligleichung ansiehst, erkennst du: Der statische Druck p muss kleiner werden, wenn die Strömungsgeschwindigkeit V zunimmt bzw. p muss ansteigen, wenn V abnimmt.

Abb. 5.1.1.5.1 Venturidüse

Obenstehend wird simuliert, wie die Luft durch eine Venturidüse (Rohr mit Verengung) strömt. An der Engstelle erhöht sich die Geschwindigkeit der Luft. Nach Start der Animation siehst du, dass die Luft dort schneller fließt.

Abb. 5.1.1.5.2 Meßanordnung Ventüridüse (Quelle: FAA Glider Flying Handbook 2013)

Im Bild oben nochmal ein Venturirohr, bei dem Geschwindigkeits- und Druckmessgeräte am Eintritt, in der Mitte und am Auslauf des Rohres angebracht sind. An der Engstelle strömt die Luft schneller und dort sinkt der Luftdruck. Im Auslauf strömt die Luft so schnell wie im Eintritt, und auch der Luftdruck ist wieder gleich.

5.1.1.6 Die Entstehung von Luftkräften an Oberflächen

Aerodynamic forces on surfaces

Du hast dich sicher schon gefragt, wie die Luftkraft bzw. der Auftrieb, der dein Flugzeug trägt, zustandekommt. Die Erklärung ist nicht so ganz einfach.

Abb. 5.1.1.6.1 Entstehung des Auftriebs

In Bild A strömt Luft durch einen breiten Kanal mit einer Querschnittsverengung. Wegen des Kontinuitäts-gesetzes ist die Strömungsgeschwindigkeit an der Stelle größer als an der Stelle . Nach dem Gesetz von Bernoulli herrscht deswegen an der Stelle ein niedrigerer statischer Druck als an der Stelle .

In Bild B setzen wir die schraffierten Körper, die die Querschnittsverengung bewirkt haben, in den freien Luftstrom. Der umströmte Körper verdrängt die Luft, sie muss um ihn herumfließen. Der Effekt ist der gleiche: An Stelle herrscht ein niedrigerer statischer Druck als an der Stelle , und zwar über und unter dem Körper.

In Bild C haben wir die untere Hälfte des Körpers weggenommen. Er ähnelt jetzt der dir bekannten Profilform. Über ihm ändert sich nichts. Der statische Druck bei ist niedriger als bei . Aber unter ihm wird kaum Luft verdrängt. Bei herrscht annähernd der gleiche statische Druck, wie bei . Was ist die Folge? Höherer Druck unter dem Körper als über dem Körper führt zu einer nach oben gerichteten Kraft. Das ist der Auftrieb. Er ist umso größer, je größer die Druckdifferenz zwischen oben und unten ist.

Zwei Dinge sollten wir uns an dieser Stelle klar machen:

Die absolute Größe des Drucks ist sowohl auf der Unterseite wie auch auf der Oberseite des umströmten Körpers positiv. Die Druckkraft drückt immer gegen die Oberfläche, ziehen kann sie nicht. Nur wird auf die Unterseite stärker gedrückt, als auf die Oberseite, wenn Auftrieb entsteht.
Vielleicht hast du irgendwo als Erklärung für die größere Strömungsgeschwindigkeit auf der Oberseite gehört, dass der Weg dort länger sei, als auf der Unterseite. Die über die Oberseite und die Unterseite strömenden Luftteilchen müssten aber gleichzeitig an der Hinterkante ankommen.
Das stimmt nicht, im Gegenteil. Ein über die Oberseite strömendes Luftteilchen erreicht die Hinterkante viel eher, als eins, das über die Unterseite fließt – trotz des längeren Weges.

Bei der Umströmung eines Körpers entsteht eine von der Körperform und der Anströmrichtung abhängige Druckverteilung.

An jedem Flächenelement ΔA der Körperoberfläche kann man also (durch Multiplikation mit dem örtlichen Druck) die dort wirkende Kraft ΔF bestimmen.

Fasst man alle örtlichen Kräfte ΔF durch Vektoraddition zu einer einzigen Resultierenden zusammen, so erhält man die resultierende Luftkraft L.

Abb. 5.1.1.6.2 Resultierende Luftkraft

Allerdings ist die Darstellung im Bild oben alles andere als maßstabsgerecht. Sie ist zwar von einer Windkanalmessung des ASK-21-Profils abgeleitet, aber so angepasst, dass du den Unterschied der Kraftelemente ΔF auf Unter- und Oberseite deutlich erkennen kannst.

Bereits in Abschnitt 5.0.2 hast du erfahren, dass man den Vektor der resultierenden Luftkraft meistens in zwei Komponenten aufspaltet. Die Auftriebskomponente – der Auftrieb – wirkt quer zur Anströmrichtung, die Widerstandskomponente – der Widerstand – parallel dazu.

Die Luftkraft und damit die beiden Komponenten ändern sich, wenn sich die Orientierung des Profils gegenüber der Anströmrichtung verändert. Man sagt, das Profil wird gegen die Anströmung angestellt. Wie groß diese Anstellung ist, misst man mit dem Anstellwinkel.

Abb. 5.1.1.6.3 Anstellwinkel

Der Anstellwinkel ist der Winkel zwischen der Anströmrichtung und der Profilsehne. Er wird mit dem griechischen Buchstaben α (alpha) bezeichnet. Die Profilsehne ist die Verbindungslinie zwischen Flügelvorder- und Hinterkante.

Vergrößert sich der Anstellwinkel, so erhöht sich die Luftkraft und damit auch der Auftrieb und der Widerstand, wobei der Auftrieb wesentlich stärker zunimmt, als der Widerstand.

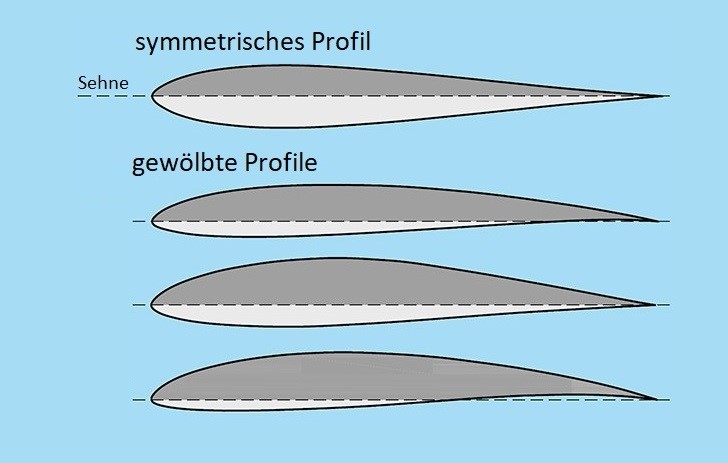
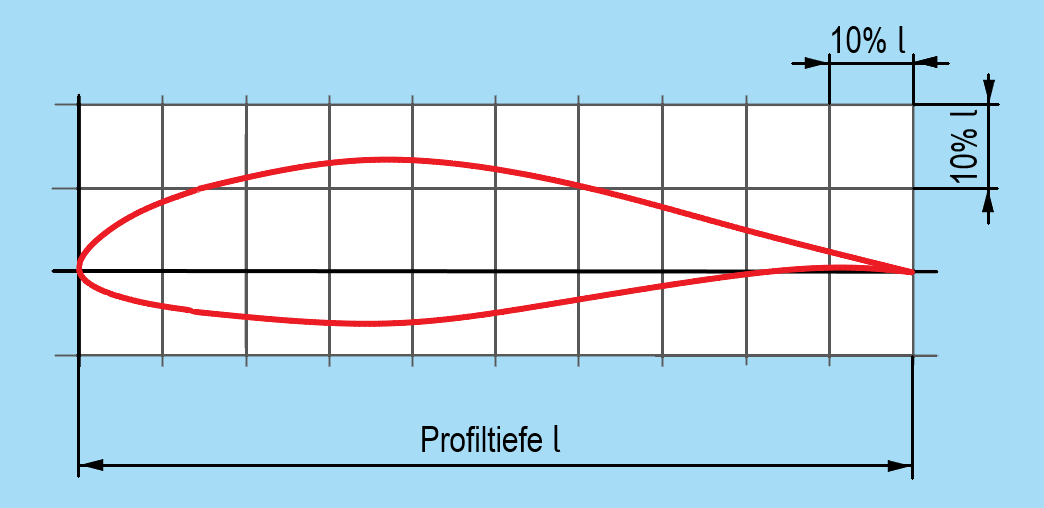
5.1.1.7 Profilgeometrie

Shape of an airfoil section

Der Flügel hat eine abgerundete Nase und eine spitz zulaufende Hinterkante. Die Nase fühlt sich ziemlich fest und steif an, die Hinterkante eher weich und biegsam. Wenn du die Ober- und die Unterseite des Flügels vergleichst, siehst du, dass die Unterseite verhältnismäßig flach und die Oberseite ziemlich gewölbt ist. Die Querschnittsform eines Flügels wird als Profil bezeichnet.

Abb. 5.1.1.7.1 Flügelquerschnitt

Es gibt verschiedene Arten von Profilen. Wir unterteilen die Profile in symmetrische und gewölbte Profile. Bei einem symmetrischen Profil. Bei einem symmetrischen Profil hat die Profilkontur beiderseits der Profilsehne die gleiche Form. Bei gewölbten Profilen ist es anders. Die Oberseite ist stark konvex, die Unterseite ist entweder relativ flach, leicht konvex, oder leicht konkav.

Abb. 5.1.1.7.2 Profilarten

Höhen- und Seitenleitwerk haben symmetrische Profile. Die Flügelprofile sind gewölbt. Wie du in der Abbildung oben siehst, können gewölbte Profile unterschiedliche Formen haben. Jedes Profil hat für einen bestimmten Zweck besonders günstige Eigenschaften.

Abb. 5.1.1.7.3 Kennzeichnende Größen eines Profils

In ein Profil kannst du entsprechend der obigen Darstellung Kreise einzeichnen. Verbindest du die Mittelpunkte der Kreise, so erhältst du die Skelettlinie des Profils. Die Verbindungslinie der Endpunkte der Skelettlinie ist die Profilsehne, oder, etwas ungenauer, die Verbindungslinie zwischen Vorder- und Hinterkante.

Die Profiltiefe l ist die Länge der Profilsehne.

Der größte Abstand zwischen Profilsehne und Skelettlinie ist die Profilwölbung, die Stelle, wo man sie findet, ist die Wölbungsrücklage. Beide gibt man meistens in Bezug auf die Profiltiefe l als Prozentangabe an.

Die Profildicke (Profilhöhe) ist der Durchmesser des größten Kreises, den du einzeichnen kannst. Auch die Profildicke kannst du in Bezug auf die Profiltiefe als Prozentangabe angeben. Oder direkt als Quotient aus Profildicke und Profiltiefe – dann bekommst du das Dickenverhältnis.

Den Anstellwinkel α kennst du schon: Er ist der Winkel zwischen der Profilsehne und der Richtung der ungestörten Anströmung, die der Bewegungsrichtung des Flugzeugs entspricht.

Sehen wir uns einmal das Profil der ASK 21 an.

Abb. 5.1.1.7.4 Profilkontur FX S 02-196

Es hat die Bezeichnung FX S 02-196. FX sind die Initialen von Professor Franz Xaver Wortmann, der das Profil entwickelt hat. S 02 ist eine interne Bezeichnung ohne besondere Aussagekraft. Hinter der Zahl 196 steckt die relative Profildicke.

Das Profil hat eine Dicke von 19,6% der Profiltiefe bei einer Dickenrücklage von 37,1%.
Die Profilwölbung beträgt 3,7%, die Wölbungsrücklage 43,5% der Profiltiefe.

Auf das ASK-21-Profil werden wir noch öfter zurückkommen.

5.1.1.8 Tragflügelgeometrie

The wing shape

Bei Segelflugzeugen kannst du diese Grundrissformen unterscheiden:

Abb. 5.1.1.8.1 Grundrissformen

Der Rechteckflügel war früher wegen des geringen Bauaufwands und seiner guten Überzieheigenschaften beliebt. Bei Segelflugzeugen kommt er nicht (mehr) zum Einsatz, weil er keine guten Flugleistungen erlaubt.
Den Trapezflügel findest du häufig bei Schul- und Übungssegelflugzeugen sowie bei Reisemotorseglern. Er ist vorteilhaft, wenn die Strukturmasse niedrig bleiben soll.
Der Rechtecktrapezflügel verspricht bessere Leistungen als der Trapezflügel, führt aber zu einer höheren Strukturmasse.
Der Doppel- oder Dreifachtrapezflügel ist heute Standard bei Segelflugzeugen, die auf gute Flugleistungen ausgelegt sind.
Der Ellipsenflügel wäre aus Leistungsgründen ebenfalls sehr interessant. Leider gelingt es in der Praxis kaum, überall die erforderliche Profiltreue einzuhalten. Dadurch geht der Vorteil leicht wieder verloren.

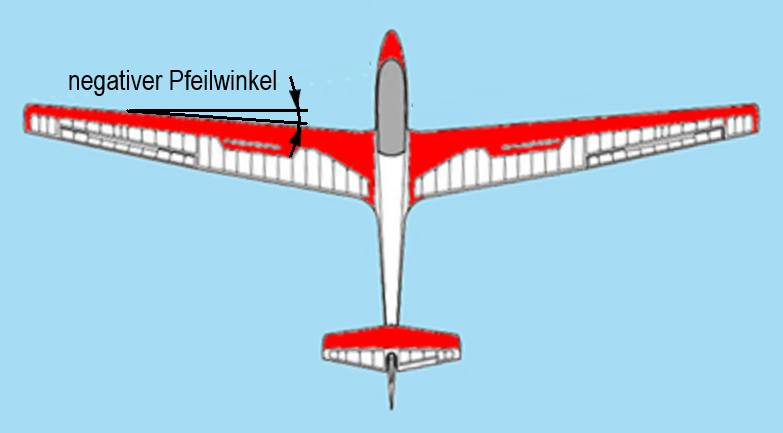
Bei manchen Flugzeugen geht die Vorderkante des Flügels leicht nach hinten. Der Flügel hat dann ein wenig die Form eines Pfeils. Wir sprechen von einer positiven Pfeilung, wenn die Vorderkante des Flügels nach hinten wegläuft.

Einige Doppelsitzer haben eine negative Pfeilung. Die Flügelspitze zeigt dann leicht nach vorn.

Abb. 5.1.1.8.2 Negative Pfeilung

Um den Grundriss genauer zu beschreiben, können folgende Angaben gemacht werden:

Abb. 5.1.1.8.3 Flügelgeometrie

Oben siehst du einen Doppeltrapezflügel mit gerader, ungepfeilter Vorderkante.

Unten ist ein gepfeilter (Einfach-)Trapezflügel dargestellt. Wenn ein Pfeilwinkel angegeben wird, musst du dich vergewissern, ob er sich auf die Vorderkante oder die l/4-Linie bezieht. Wie der Name sagt, findest du die l/4-Linie bei 25% Flügeltiefe. Diese Stelle ist aerodynamisch von gewisser Bedeutung. Wir werden später darauf zurückkommen.

Abb. 5.1.1.8.4 V-Stellung

Wenn die Flügelhälften rechts und links leicht nach oben weisen, sprechen wir von der V-Stellung des Flügels. Sie wird gegenüber der Horizontalebene gemessen und in Grad angegeben. Ein Flugzeug mit V-Stellung fliegt stabiler (wird unter 5.3 erläutert), und bei Start und Landung gibt es mehr Abstand zwischen Flügelspitze und Boden.

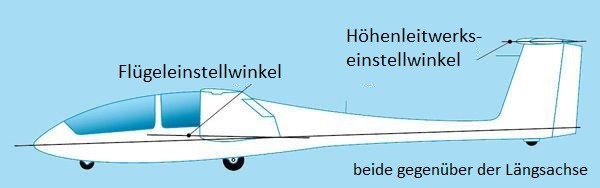
Abb. 5.1.1.8.5 Einstellwinkel

Die Gerade von der Hinterkante zur Profilnase ist die Profilsehne. Der Winkel der Profilsehne mit der Flugzeuglängsachse ist der Einstellwinkel. Dieser Winkel ist vom Konstrukteur festgelegt. Dabei hat er darauf geachtet, dass der Rumpfwiderstand in den normalen Fluglagen möglichst klein ist. Außerdem ist der Einstellwinkel maßgeblich für den Bodenanstellwinkel des Flügels. Das Segelflugzeug soll mit niedriger Geschwindigkeit abheben und aufsetzen können, trotzdem müssen die Querruder beim An- und Ausrollen ausreichend wirksam sein.

Auch die Profilsehne des Höhenleitwerks bildet einen Winkel mit der Rumpflängsachse. Der Höhenleitwerkseinstellwinkel ist kleiner als der Flügeleinstellwinkel. Vergleicht man Flügeleinstellwinkel und Höhenleitwerkseinstellwinkel miteinander, so erhält man die Einstellwinkeldifferenz.

Verwechsle den Einstellwinkel nicht mit dem Anstellwinkel!

Die ASK 21 hat einen Doppeltrapezflügel mit diesen Daten:

Spannweite	17,00 m
*Wurzeltiefe*	1,50 m
Knickstelle bei y =	5,20 m
Tiefe am Flügelknick	1,00 m
Außenflügeltiefe	0,50 m
Pfeilwinkel (Vorderkante)	0°
V-Stellung	+ 4°
Einstellwinkel	+ 2°

Anker: Drücke = gdfgr2; Geschwindigkeit = gdfgr3; Kontinuität = gdfgr4; Bernoulli = gdfgr5; Luftkräfte = gdfgr6; Profilgeo = gdfgr7; Tragflügelgeo = gdfgr8

xxxxxxx

Details: Geschrieben von Super User; Erstellt: 02. Dezember 2020; Zuletzt aktualisiert: 11. Juni 2024; Zugriffe: 16982