9.1 Grundlagen der Navigation
Basics of navigation
Inhalt dieses Kapitels:
Als unentbehrliche Hilfsmittel in der Luftfahrt – Navigation benötigst Du eine Karte und einen Kompass. In den letzten Jahren kommen auch verstärkt GPS-Empfänger in Kombination mit Streckenflugrechnern zum Einsatz.
In Deutschland verwenden wir als Luftfahrtkarte die sogenannte ICAO-Karte.
Beim Studium dieses Kapitels, beim Lernen, bei der SPL-Prüfung und auch beim praktischen Fliegen soll diese Karte immer dabei sein.
9.1.1 Das Koordinatensystem
Wenn du im Internet auf der Seite https://www.gpskoordinaten.de an einem beliebigen Ort auf die Karte klickst, erhält du die Koordinaten dieses Ortes.
Diese werden dir hier in Gradzahlen mit Dezimalstellen angeben.
Eine weitere Möglichkeit ist die Angabe in Grad, Minuten und Sekunden, welche du weiter unten, links auf der Seite ebenfalls findest. Luftfahrtkarten, wie z.B. unsere ICAO-Karte, verwenden diese Form der Angaben.
Nachfolgend soll dir nun etwas näher erklärt werden, wie die Positionierung nach Grad, Minuten und Sekunden funktioniert.
 Abb. 9.1.1.1 DAEC Braunschweig
Abb. 9.1.1.1 DAEC Braunschweig
Wenn du in https://www.gpskoordinaten.de wie in unserem Beispiel oben den Standort des DAeC in Braunschweig suchst, werden dir die dazugehörigen Koordinaten angezeigt. Wir nehmen natürlich gleich die Angabe in Grad, Minuten und Sekunden, da wir uns ja an diese gewöhnen wollen:
52°18‘52‘‘ N (North) und 10°32‘50‘‘ E (East)
Dies funktioniert übrigens auch mit anderen Programmen und Diensten, wie z.B. Google Maps.
Die Erde ist annähernd eine Kugel, die sich in 24 Stunden einmal um die Erdachse dreht. Diese Achse ist eine imaginäre Achse, die wir uns nun vorstellen. Der obere Endpunkt dieser Achse wird als geographischer Nordpol und der untere Endpunkt als geographischer Südpol bezeichnet. Vom Nordpol aus betrachtet, dreht sich die Erde entgegen dem Uhrzeiger - also von Westen nach Osten.
 Abb. 9.1.1.2 Bild der Erde (Animierte Darstellung)
Abb. 9.1.1.2 Bild der Erde (Animierte Darstellung)
9.1.1.1 Die Erde
Die Erde kreist in einem Jahr einmal um die Sonne. Dazu benötigt sie 365,25 Tage, und somit hat ein Jahr i.d.R. 365 Tage und jedes vierte Jahr 366 Tage (Schaltjahr). Da die Erdachse, in Bezug auf die Sonnen-Umlaufebene, nicht senkrecht zur Sonne steht, sondern um etwa 23,5° gekippt ist, gibt es die uns bekannten vier Jahreszeiten.
9.1.1.2 Meridiane, Breiten- und Großkreise
Um es uns zu ermöglichen einen beliebigen Standort auf der Erde zu bestimmen, stellen wir uns zur Hilfe Linien auf ihr vor. Diese spannen wir einmal von Nord nach Süd sowie von Ost nach West auf, sie schneiden sich also in einem Winkel von 90°.
Die Nord-Süd-Linien nennen wir Meridiane, die Ost-West-Linien Breitenkreise bzw. –parallelen.
Wenn du dir die Erde gedanklich wie eine Orange vorstellst und sie von oben nach unten in zwei Teile schneidest, dann siehst du, dass zwei sich gegenüberliegende Meridiane einen Kreis bilden. Die Schnittebene verläuft hierbei durch den Mittelpunkt.
Ein solcher Kreis, dessen Ebene durch den Mittelpunkt der Erde verläuft nennen wir Großkreis (Orthodrome). Diese teilen die Erde immer in zwei gleich große Hälften, sie sind daher auch alle gleich groß.
Wenn du die Erde nun so schneidest, wie auch normalerweise eine Orange zum Auspressen, erhältst du den größeren Breitenkreis. Er würde bei der Erde dem Äquator entsprechen. Wir sehen wieder einen Großkreis.
Der Mittelpunkt aller Großkreise ist der Mittelpunkt der Erde und sie teilen die Erde immer in zwei gleich große Hälften!
9.1.1.3 Kleinkreise
Im Gegensatz hierzu gibt es aber auch Kreise deren Mittelpunkt nicht durch den Erdmittelpunkt verläuft. einen solchen Kreis nennen wir Kleinkreis.
Unser größter Breitenkreis ist der Äquator. Er ist ein Großkreis mit etwa 40.000 km Umfang.
Zu den beiden Polen hin nimmt der Umfang der Breitenkreise stetig ab und der Schnittpunkt dieser kleineren Kreise geht nicht mehr durch den Mittelpunkt der Erde.
Auf einer Höhe von 23° 26' Nord oder Süd spricht man von den Wendekreisen (Sonnenstand erreicht an der Sonnenwende die Senkrechte), die Höhe 66° 33' markiert die Polarkreise (ab hier geht an der Sonnenwende die Sonne nicht mehr auf oder unter).
Der Äquator ist die Hauptlinie in Ost-West-Richtung.
Der Nullmeridian, der durch die Sternwarte im britischen Greenwich verläuft, ist die Hauptlinie in Nord-Süd-Richtung.
Alle Linien, die parallel zum Äquator verlaufen, sind die Breitenparallele, auch Breitenkreise genannt.
Die Linien, die in Nord-Süd-Richtung verlaufen, sind die Meridiane oder Längenkreise.
9.1.1.4 Hemisphären
Der Nullmeridian über Greenwich und der 180°-Meridian teilen die Welt in eine westliche und eine östliche Halbkugel, die sogenannten Hemisphären.
Deutschland befindet sich damit auf der östlichen Hälfte der Welt. Wir zeigen dies mit dem E vom englischen East an.
Der Äquator wiederum teilt die Welt in eine nördliche und eine südliche Hemisphäre.
Deutschland liegt auf der nördlichen Hemisphäre und dies wird mit dem N von Nord (bzw. North) angegeben.
9.1.1.5 Zusammenfassung
Die Welt hat annähernd die Form einer Kugel.
Der Äquator, blau in der Abbildung dargestellt, ist ein Kreis mit 360°.
Meridiane oder Längengrade
Der Nullmeridian, hier in Rot eingezeichnet, verläuft quer durch Greenwich in Großbritannien. Von der Stelle aus, an der der Nullmeridian den Äquator kreuzt, zählen wir 180 Meridiane (Grad) nach Osten ab.
Diese kannst du auch in der Abbildung sehen. Jeweils im Abstand von 10 Meridianen (Grad) ist immer einer dargestellt.
9.1.1.6 Längengrade und Zeit
Wir erinnern uns, der Umfang der Erde beträgt etwa 40.000 km. Exakt sind es 21600 Nautische Meilen.
Die Sonne geht im Osten auf, um 12 Uhr steht Sie auf der Nordhalbkugel genau im Süden, im Westen geht Sie unter.
In 24 Stunden dreht sich die Erde einmal um ihre Achse. In einer Stunde dreht sich die Erde also um 15 Grad (360°/24h).
Alle 15 Grad beginnt theoretisch immer eine andere Zeitzone. In der Realität ist dies jedoch nicht überall so, da die Einteilung der Zeitzonen auch häufig Ländergrenzen nutzt bzw. sich daran orientiert.
Du kannst dir sicherlich vorstellen, dass es für ein Land, natürlich praktischer ist nur eine Zeitzone zu haben, insofern dies möglich ist.
 Abb. 9.1.1.12 Zeitzonen (zur Vergrößerung auf das Bild klicken)
Abb. 9.1.1.12 Zeitzonen (zur Vergrößerung auf das Bild klicken)
In der Luftfahrt werden alle Zeiten einheitlich in einer koordinierten Weltzeit angegeben. Sie wird mit UTC (Universal Time Coordinated) bezeichnet. Dies ist die Standardzeit, welche auf einer Atomuhr basiert.
Wie in Abb. 9.1.1.12 gezeigt gibt es viele Zeitzonen. Dazu kommt noch die Umstellung auf Sommer- bzw. Winterzeit. So ist z.B. MEZ (Mitteleuropäische Zeit) um 1 Stunde größer als UTC und MESZ (Mitteleuropäische Sommerzeit) um 2 Stunden größer als UTC.
9.1.1.7 Koordinatensystem und Abstände
Wie im Kapitel 9.1.1 bereits kurz erwähnt, verfeinert das Koordinatensystem die Gradzahlen weiter auf Minuten und Sekunden um zu einer genaueren Angabe zu kommen. So entspricht 1° exakt 60‘ (Winkelminuten) und 1‘ exakt 60“ (Winkelsekunden). Dies ist vergleichbar mit der Zeiteinteilung auf einer Uhr.
Der Abstand von einem Grad (also zwischen zwei Längengeraden) entspricht auf dem Äquator und zwischen den Breitengraden (also entlang der Meridiane nach Nord und Süd) einer Länge von 60 nautischen Meilen (NM) oder im metrischen System 111 km (40.000 km : 360° = 111 km pro Grad). Entsprechend ergibt 1‘ oder (1/60)° exakt 1 nautische Meile (NM), man spricht auch von der Bogenminute. Umgerechnet in das metrische System ergibt dies 1852 Meter bzw. 1,852 km (40000 km / 21600 NM).
Will man nun den Abstand (als Winkel) zweier Punkte mit gleicher Breite und unterschiedlicher Länge oder gleicher Länge und unterschiedlicher Breite auf der Erde in Grad, Minuten und Sekunden ermitteln so muss man diese Werte voneinander subtrahieren.
Z.B. Ort A 04° 14,5‘ E Ort B 02° 30,5‘ E
Dies ist nicht ganz einfach, die Überträge sind anders als bei Zahlen im metrischen System:
Rechnung: Von 02° 30,5‘ W auf 03° 00‘ W sind es 29,5‘.
Dies gilt solange beide Werte auf derselben Hemisphäre (Kap 9.1.1.4) sind, bei unterschiedlichen Hemisphären sind die Werte zu addieren.
Rechnung: 15° 29,3‘ N + 8° 14,7‘ S ergibt einen Abstand von 23° 44‘.
9.1.1.8 Breitenkreise oder Breitenparallele
Parallel zum Äquator verlaufen die Breitenkreise, auch Breitenparallelen genannt. Sie beschreiben den Abstand vom Äquator.
Diese sind stets parallel zueinander und sind imaginäre horizontale Linien, die in Ost-West-Richtung über den Globus verlaufen.
Vom Äquator bis zum Nordpol sind es 90 Grad. Wir zählen hier 89 Breitenkreise vom Äquator nach Norden. Ebenso sind es 89 Breitenkreise in die andere Richtung zum Südpol. Der Nordpol und der Südpol selbst sind nur Punkte.
Es gibt also 2 x 89 Breitenkreise. Vom Nordpol zum Südpol beträgt der Winkel somit 180° (90°.N.+.90°.S).
Beträgt der Unterschied zwischen zwei Breitenkreisen genau ein Grad dann haben die den Abstand von einem Breitengrad.
Der Abstand zwischen zwei Breitengraden beträgt bekanntermaßen 60 NM.
Oben auf der Abbildung unserer Weltkugel sieht du, dass auch hier jeder 10. Breitengrad dargestellt wird.
Dieses System aus Meridianen und Breitenkreisen ermöglicht es dir also nun jeden Ort auf der Erde genau zu bestimmen.
Wir machen das, indem wir den zugehörten Breitengrad und Längengrad eines Punktes angeben. Liegt der Punkt beispielsweise nördlich des Äquators, nennen wir ihn nördliche Breite. Wenn er dazu östlich von Greenwich liegt, bekommt er die weitere Bezeichnung östliche Länge.
Der Breitengrad und der Längengrad eines Punktes werden als seine Koordinaten bezeichnet.
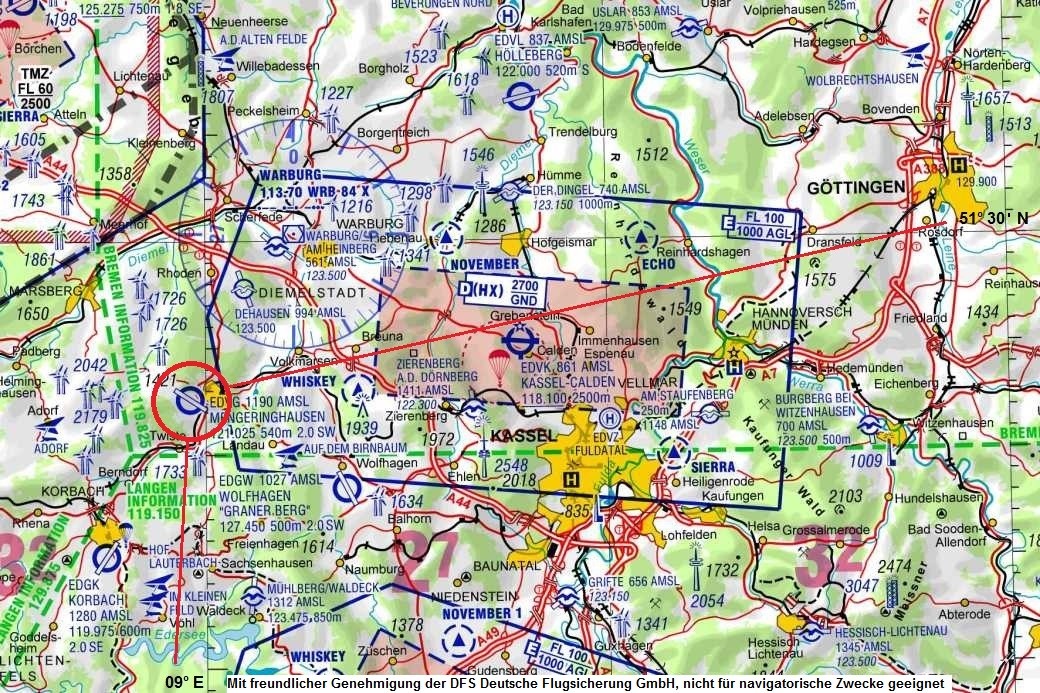
Auf dem Kartenausschnitt unten (ICAO-Kartenblatt Hannover) kannst du sehen, dass der Flugplatz Mengeringhausen ungefähr auf 51°22‘ nördlicher Breite und 9° östlicher Länge liegt.
Du kommst zu dieser Aussage indem du feststellst, dass sich der Punkt Mengeringhausen hierbei etwas unterhalb der 51° 30' N-Linie und etwas westlich der 9°E-Linie befindet.
Ziehen wir hier die AIP zu Rate, verrät dir diese, dass der Flugplatz Mengeringhausen sich auf der genauen Position 51° 22,59'N und 008°58,87'E befindet.
Es wird immer zuerst die Breite und dann die Länge angegeben.
Für die Ermittlung der genauen Position, teilen wir die Gradzahl in 60 Minuten und die Minuten in 60 Sekunden auf. Das jeweilige Zeichen hinter der Zahl hierfür ist:
- Grad ist: (°),
- Minuten: (')
- Sekunden: ('')
Für die Ermittlung der genauen Position aus der Karte suchen wir uns den am nächsten gelegenen Breitenkreis, dieser ist hier 51° 30“ N. Mit einem Lineal parallel zum Breitenkreis durch Mengeringhausen gelegt können wir ca. 7 Bogenminuten am Meridian ablesen, also abziehen. Das gleiche machen wir für den Längengrad und sehen hier, dass Mengeringhausen kurz vor dem Längengrad 09° E liegt, wir ziehen hier also 1 Minute ab.
Die Sekunden können auf dieser Karte nicht gezählt werden, dazu ist der Maßstab nicht geeignet.
9.1.2 Die Kompassrose
In der Luftfahrt werden Richtungen in Grad angegeben.
Zur besseren Veranschaulichung und Orientierung nehmen wir uns hier die Kompassrose zur Hilfe. Sie ist ein Kreis bezogen auf die Himmelsrichtungen und unterteilt in 360°. Daraus ergeben sich die Haupthimmelsrichtungen mit N = 000°, S=180°, O=090° und W=270°.
Auf der Magnetkompassrose wird bei der Beschriftung allerdings aus Platzgründen und zur besseren Übersicht die letzte 0 weggelassen, aus 060° wird daher 06 usw.
Auf einem Flughafen ist an den Köpfen, also am Beginn der Piste immer die Richtung angegeben, in welche du auch startest oder landest. Allerdings sind auch hier nur die ersten zwei Stellen angegeben, die Angaben beziehen sich immer auf magnetisch Nord (MN) und sind auf die nächsten 10° gerundet. Das ist sehr praktisch denn die Ziffernfolge auf der Piste muss immer den Ziffern auf dem Kompass entsprechen!
D.h. wenn du auf dem Flughafen Sylt z.B. in östlicher Richtung landest, nimmst du die Piste 06. Startest du auf der langen Piste in Richtung Südosten wählst du die Piste 14, um in Richtung 140° zu starten.
9.1.2.1 Variation
Der Kurs, den wir aus unserer Luftfahrtkarte entnehmen wird rechtweisender Kurs (rwK) genannt (oft auch als Wahrer Kurs bezeichnet, von der englischen Bezeichnung True Course). Dieser bezieht sich, wie auch unsere Karte, auf den geographischen Nordpol (GN), oder anders ausgedrückt entlang einer Orthodrome (Längenkreis) welche ja zum geographischen Nordpol führt.
In der Nähe des geographischen Nordpols (GN) liegt der magnetische Nordpol (MN). Die Nadel unseres (magnetischen) Kompasses zeigt auf ihn. Die vom Kompass angezeigte Richtung hat daher eine Abweichung zum geographischen Norden und diese Abweichung ist je nach Ort an dem wir uns befinden unterschiedlich!
Es gibt 3 verschiedene Begriffe für diese Abweichung: Missweisung (MW), Ortsmissweisung (OM) oder Deklination, alle 3 sind identisch. Im weiteren Text bleibt es bei (OM). Der englische Begriff ist die variation (VAR).
Um vom jetzt vom geplanten rechtweisenden Kurs (rwK) auf den missweisenden Kurs (mwK) umzurechnen muss man die (OM) unter Berücksichtigung des Vorzeichens subtrahieren. Wie man in Abbildung 9.1.2.5 sehen kann bedeutet eine westliche Ortsmissweisung, dass unser Magnetkompass kleiner anzeigt, man muss also größer steuern um zum rechtweisenden Ziel zu kommen. Genau umgekehrt ist es bei einer östlichen Ortsmissweisung, hier wird der Magnetkompass größer anzeigen, man muss entsprechend kleiner steuern.
|
OM West (-) OM Ost (+)
GN - OM =MN
und als Kurs
rwk - OM = mwk |
Abb. 9.1.2.5 Ortsmissweisung |
Der magnetische Nordpol wandert im Laufe der Zeit allerdings, damit verändert sich natürlich auch die Abweichung zum geographischen Nordpol. Diese Abweichung muss aus der aktuellen Luftfahrtkarte entnommen werden wo sie bei jeder Neuauflage auch entsprechend korrigiert wird.
9.1.2.2 Isogonen
Beim näheren Blick auf die ICAO-Karte kannst du eine oder mehrere schwarz gestrichelte Linien finden, welche von oben nach unten verlaufen und mit einer Gradzahl ° und zusätzlich einem W oder einem E gekennzeichnet sind. Diese Linien werden Isogone genannt und sie verbinden Punkte, bei denen die Ortsmissweisung gleich groß ist. In Deutschland beträgt diese (OM) im Jahr 2021 zwischen 2° Ost und 4° Ost, sie ist damit relativ gering und sie ändert sich auch nur relativ langsam.
9.1.2.3 Deviation
Da unser Magnetkompass, genauer dessen Nadel magnetisch ist, wird seine Anzeige durch magnetische oder metallische Teile sowie elektrische Leitungen in der näheren Umgebung beeinflusst.
Diese Abweichung wird als Kompassfehler oder Deviation (DEV) bezeichnet. Sie ist der Winkel um den deine Kompassanzeige (Kompass Nord oder KN) von magnetisch Nord (MN-> mwN) abweicht.
Jedes Flugzeug hat hier unterschiedliche Abweichungen, je nach Konstruktion und Einbau von Instrumenten und Elektrik. Daher findest du diese in einer dem Kompass zugehörigen Tabelle, auch Deviationstabelle genannt. Es gibt zwei Arten davon, siehe Abb. 9.1.2.6 unten. In ihr ist beschrieben, wie groß die jeweilige Abweichung bezogen auf eine bestimmte Richtung ist.
Wenn man also nach Kompass Nord fliegt ergibt sich:
MN – DEV = KN..........und als Kurs ausgedrückt..........mwK – DEV = KK
Abb. 9.1.2.6 Deviationstabellen
9.1.3 Kursbestimmung
Die Kursbestimmung ist in der Navigation von grundlegender Bedeutung und gleichzeitig durch die Vielzahl der Begriffe und notwendigen Berechnungen alles andere als einfach zu verstehen. Es wird einige Zeit dauern und manche Wiederholung notwendig werden bis alles für die Theoretische Prüfung sitzt.
Abschnitte
9.1.3.1 Die Kursgleiche (Loxodrome) und der Großkreis (Orthodrome)
Willst du auf der Karte den Kurs deines geplanten Fluges bestimmen, so zeichnest du zuerst eine Linie von deinem Startpunkt A zum Zielpunkt B. Dann misst du mit Hilfe eines Kursdreiecks an dem Meridian, welcher der Mitte deiner Linie am nächsten ist, die Gradzahl deines Kurses in Richtung Zielpunkt heraus.
Du fragst dich sicher warum das so gemacht wird. Um das besser zu verstehen, befassen wir uns nun als erstes mit den sogenannten Kursgleichen (Loxodrome) und Großkreisen (Orthodrome).
Eine Kursgleiche, auch als Loxodrome bezeichnet, ist eine Linie auf der Erdoberfläche entlang derer der Kurs stets gleich ist. D.h. folgst du dieser von A nach B entlang, so wird auf der gesamten Stecke stets mit dem gleichen Kurs geflogen. Daher auch der Name Kursgleiche.
Eine solche Linie nähert sich dem Pol spiralförmig.
Abb. 9.1.3.1 Loxodrome und Großkreis
Kursgleiche (Loxodrome, rot) und Großkreis (Orthodrome, blau)
Fliegst du in der Abbildung von A nach B und folgst dabei der roten Linie, siehst du, dass diese alle Meridiane im gleichen Winkel schneidet. In diesem Fall folgt dein Kurs dem einer Kursgleichen bzw. Loxodrome.
Das hat zwar den Vorteil, dass du nie den Kurs ändern musst. Der Nachteil jedoch ist, dass dies nicht der kürzeste Weg zwischen zwei Punkten auf unserer Erdkugel ist.
Verwendest du hingegen die blaue Linie des Großkreises als Verbindungslinie von A nach B, erhältst du nun den kürzesten Weg zwischen den zwei Punkten. In den von uns verwendeten Flugkarten entspricht dies einer geraden Linie (siehe Kapitel 9.3 Flugkarten).
Du stellst aber auch fest, dass diese Kurslinie die Meridiane nun jedes Mal in einem anderen Winkel schneidet. Auf einer solchen Großkreisroute musst du deinen Kurs regelmäßig anpassen, denn der Winkel zu den Meridianen ändert sich hier ständig. Besonders wichtig ist dies bei langen Ost-West und West-Ost Strecken wie sie typischerweise in der kommerziellen Luftfahrt auftreten.
Bei kurzen Strecken sowie Strecken, die eher in Nord-Süd- oder Süd-Nord-Richtung verlaufen, ist die Abweichung dagegen gering.
Beim Segelfliegen zeichnen wir auf unserer Karte daher eine gerade Linie von A nach B. Dieses ist die kürzeste Strecke. Damit folgst du dem Abschnitt eines Großkreises, der zwischen A und B verläuft und dann vollends die Erde umrundet.
9.1.3.2 Vom rechtweisenden Kurs (rwK) zum Kompasskurs (KK)
Möchtest du im richtigen Flug von A nach B fliegen, musst du zusätzlich die Ortsmissweisung (Variation) und die Deviation in deiner Kursbestimmung berücksichtigen, denn der Magnetkompass zeigt bekanntlich nicht den Rechtweisenden Kurs (rwK) an.
In der Abbildung siehst du, dass sich die Winkel deines Kompasskurses (KK), nach dem du dein Flugzeug steuerst, und der des Kurses aus deiner Karte (rwK) unterscheiden.
Kursumrechnung (rwK nach KK)
Um den aus der Karte abgelesenen Kurs in den zu fliegenden Kompasskurs umzurechnen, muss nach folgendem Schema vorgegangen werden:
1. Berechnung des missweisenden Kurses:
- rwK - OM = mwK (rechtweisender Kurs – Ortsmissweisung = missweisender Kurs)
2. Berechnung des Kompasskurses:
- mwK - DEV = KK (missweisender Kurs – Deviation = Kompasskurs)
Merke:
- Abweichung Ost ist immer positiv (+), d.h. der Kompass zeigt zu viel an, der Wert muss also in der Rechnung oben abgezogen werden (+ mal - = -)
- Abweichung West ist immer negativ (-), Kompass zeigt zu wenig an, der Wert muss also oben addiert werden (- mal - = +)
Beides gilt für die Ortsmissweisung als auch für die Deviation, wobei die Deviation in der Deviationstabelle in der Regel das Vorzeichen bereits enthält (siehe Abb. 9.1.2.6 rechts).
Beispiel:
Nehmen wir an, der Kurs auf der Karte beträgt 90°. Die Ortsmissweisung ist +3° (Ost) und die Deviation laut Deviationstabelle -5°.
Wie lautet der Kompasskurs den du somit fliegen musst?
| rwK | -OM | mwK | -Dev | KK |
| 90 ° | -(+3 °) | 87 ° | -(-5 °) | 92 ° |
Kursumrechnung (KK nach rwK)
Willst du dir umgekehrt nun den rwK aus dem Kompasskurs herleiten, drehst du die Rechnung von zuvor einfach wie folgt um und beachte dabei das sich aus der Subtraktion eine Addition ergibt.
1. Berechnung des missweisenden Kurses:
- KK + DEV = mwK
2. Berechnung des rechtweisenden Kurses:
- mwK + OM = rwK
| KK | +Dev | mwK | +OM | rwK |
| 92 ° | +(-5 °) | 87 ° | +(+ 3 °) | 90 ° |
9.1.3.3 Das Winddreieck
Da es auf deinen Flügen meist nicht windstill sein wird, musst du bei der Bestimmung deines Kurses neben der Ortsmissweisung und der Deviation auch die Windrichtung und –stärke mitberücksichtigen, denn der Wind wird dich vom geflogenen Kurs abtreiben!
Windeinfluss ungeplant
Fliegen wir mit Seitenwind stimmen der Steuerkurs (SK) und der Kurs über Grund (KüG) nicht mehr überein.
Der Wind von der Seite trägt dich von deinem Kurs weg. Diese seitliche Versetzung wird Abdrift genannt. Der Abdriftwinkel ist folglich der Winkel, um den dich der Wind zu deinem geplanten Kurs versetzt.
Beachte bitte die Pfeilspitzen der Abbildung, sie zeigen die Richtung an und die Länge entspricht der Geschwindigkeit.
Eine Spitze bezeichnet den Steuerkurs-Vektor – rwSK und VE
Zwei Spitzen bezeichnen den Grund-Vektor – rwK und VG
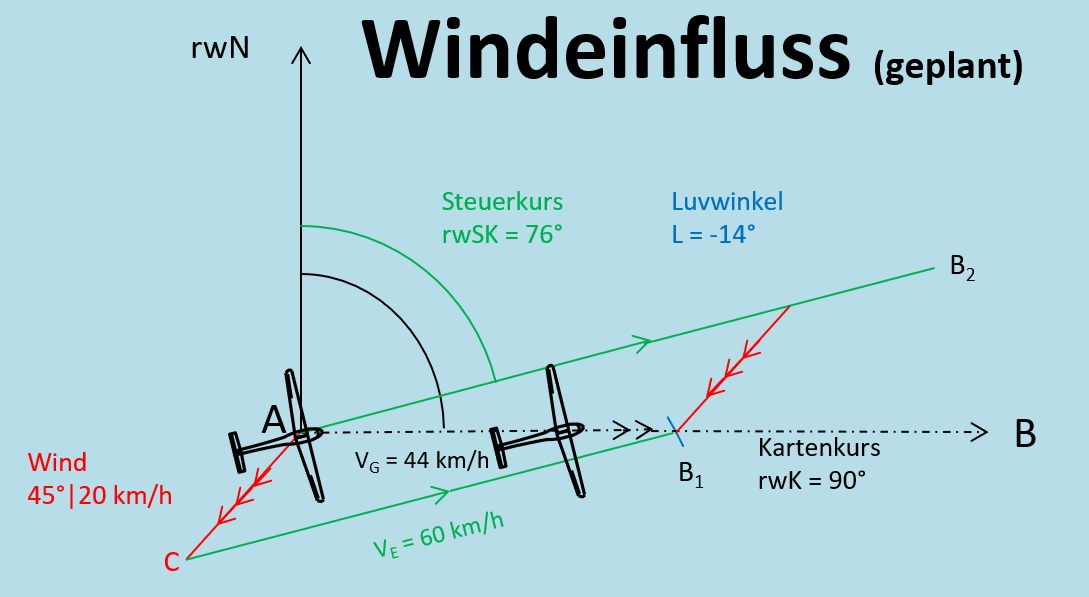
Windeinfluss geplant
Nehmen wir an, du hast auf deiner Karte einen rwK von 135° ermittelt. Der Wind ist kräftig und kommt fast genau seitlich zu deinem Flugweg. Um auf deinem ursprünglichen Kurs aus der Karte zu bleiben, musst du nun beachtlich gegensteuern.
Wie stark hängt von folgendem ab:
- der Eigengeschwindigkeit VE
- der Windstärke VW
- der Windrichtung WR
Die Eigengeschwindigkeit VE entspricht deiner angesetzten mittleren Reisegeschwindigkeit für den Überlandflug.
Angenommen du willst von Punkt A nach Punkt B fliegen. Der Kartenkurs rwK beträgt 135°.
Der Wind kommt von Links aus der Richtung 060° und beträgt 20 km/h.
Welchen Steuerkurs rwSK solltest du dann bei einer erwarteten Eigengeschwindigkeit Ve von 60 km/h fliegen?
Du hast damit folgende Angaben:
- rwK 135°
- Wind aus 60°
- Windstärke 20 km/h
- Reisegeschwindigkeit VE 60 km/h
Anhand dieser Angaben kannst du mit Hilfe eines Navigationsrechners oder eines Navigationsprogramms deinen Steuerkurs ermitteln, du kannst dies aber auch mit Hilfe von Kursdreieck und Zirkel zeichnerisch lösen. So gehts:
Abb. 9.1.3.4 Graphische Konstruktion Winddreieck
Als erstes zeichnest du mit dem Kursdreieck den rechtweisenden Kurs aus der Karte von A nach B in Richtung 135° auf und markierst ihn mit einem Pfeil (die schwarz gestrichelte Linie in der Abbildung). Zusätzlich zeichnest du im Punkt A einen Meridian nach rwN.
Als nächstes zeichnest du den Wind mit seiner Richtung und Stärke ein und markierst mit drei Pfeilen.
Eine Windstärke von 20 km/h wird hier durch eine Länge von 2 cm dargestellt.
Ein Segelflugzeug, das sich über Punkt A befindet, wird unter dem Einfluss des Windes innerhalb einer Stunde zum Punkt C abgetrieben. Diesen Punkt nennt man daher auch Windstillepunkt.
Das Flugzeug hat eine Eigengeschwindigkeit von 60 km/h.
Diese Information verwendest du nun in der Zeichnung indem wir einen Zirkel auf 6 cm (Maßstab: 1 cm = 10 km/h) einstellen und vom Punkt C aus, einen Kreisbogen ziehen, der in diesem Abstand die Linie AB schneidet. Den Schnittpunkt bezeichnest du mit B1.
Du kannst nun die Geschwindigkeit über Grund Vg anhand der Länge der Linie AB1 und unserem Maßstab ablesen. Sie beträgt 51 km/h. Mit dieser Geschwindigkeit bewegst du dich unter Einfluss des Windes tatsächlich gegenüber dem Boden voran.
AB1C ist das Winddreieck.
CB1 ist die Richtung des zu fliegenden rechtweisenden Steuerkurses. Nun nimmst du als Ausgangspunkt jedoch den Punkt A anstatt Punkt C und verschiebst die Linie parallel dorthin zu AB2. Dies ist der Steuerkursvektor und wird mit zwei Pfeilen markiert.
Der Winkel, den du mit dem Kursdreieck zwischen den Linien AB1 und AB2 misst (in dem Beispiel 18°), ist der Winkel, den du vorhalten musst (hier nach Norden, also minus) um die Abdrift durch den Wind auszugleichen. Er wird Luvwinkel genannt.
Merke: Kommt der Wind von rechts musst du grösser steuern, der Luvwinkel ist also positiv, kommt der Wind von links musst du kleiner steuern und der Luvwinkel ist negativ.
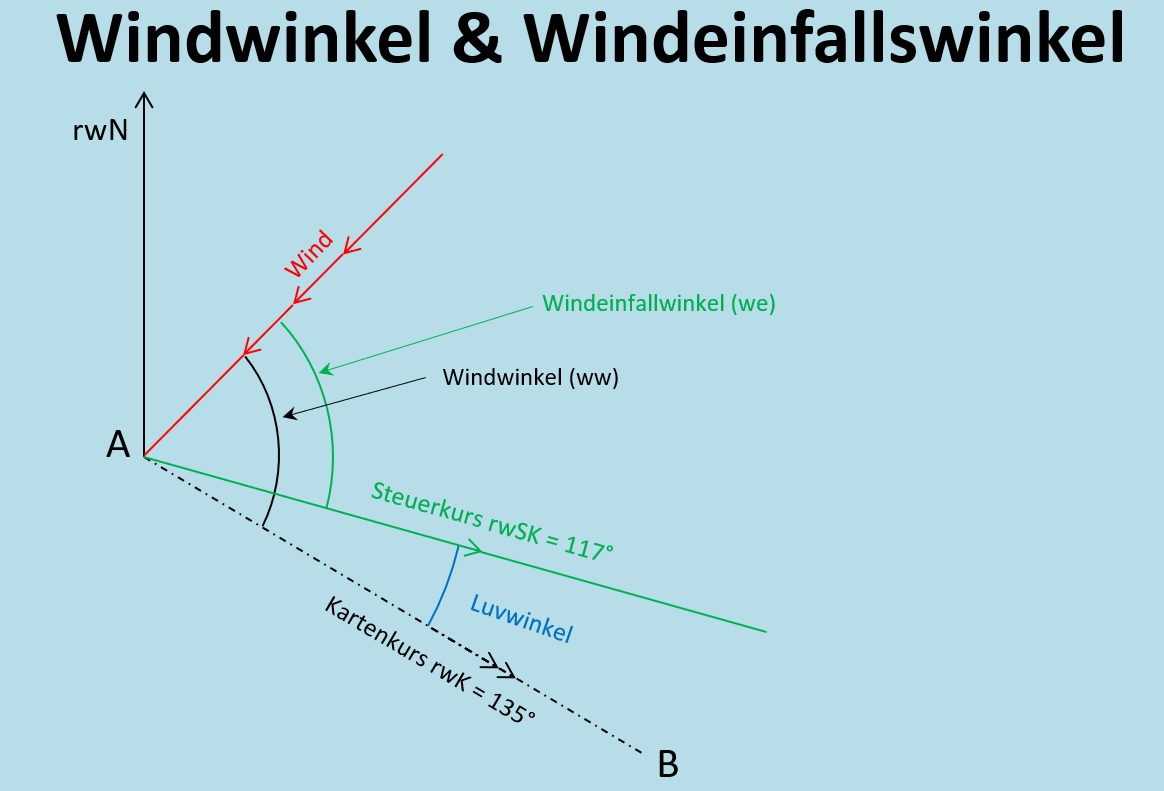
9.1.3.4 Windwinkel
Im Kapitel zuvor hast du schon den Einfluss des Windes kennengelernt und den Luvwinkel sowie die Abdrift bestimmt. Es gibt hierzu noch zwei weitere Winkel welche Du eventuell bei deiner Prüfung beantworten musst.
Der Windwinkel (ww)
Winkel zwischen dem rechtweisenden Kurs und der Richtung aus der der Wind kommt. Nach rechts 0° - 180° positiv, nach links 0° - 180° negativ.
Der Windeinfallswinkel (we)
Winkel zwischen dem rechtweisenden Steuerkurs und der Richtung aus der der Wind kommt. Nach rechts 0° - 180° positiv, nach links 0° - 180° negativ.
9.1.3.5 Vollständiges Kursdiagramm
9.1.3.6 Vom rwK zum KSK und zurück
9.1.3.7 Zusammenfassung Begriffe
In der Navigation gibt es sehr viele Begriffe und die Gefahr diese zu verwechseln ist gross. Daher hier nochmals eine Zusammenfassung aller wichtigen Begriffe und ihrer Abkürzungen sowohl in Deutsch als auch in Englisch.
Bezugsrichtungen
rwN - Rechtweisend Nord TN - true north
mwN - Missweisend Nord MN - magnetic north
KN - Kompass Nord CN - compass north
Beschickungen
MW, OM - Missweisung oder Ortsmissweisung VAR - variation
Dev - Deviation DEV - deviation
Geschwindigkeiten und Richtungen
VE - Eigengeschwindigkeit TAS - true airspeed
VG - Geschwindigkeit über Grund GS - groundspeed
VW - Windgeschwindigkeit WV - wind velocity
WR - Windrichtung WD - wind direction
Kurse und Windeinfluß
rwK - Rechtweisender Kurs auch Kartenkurs TC - true course
mwK - Missweisender Kurs MC - magnetic course
KK - Kompasskurs CC - compass course
A - Abdrift (geplant) DA - drift angle
L - Luvwinkel WCA - wind correction angle
DZ - zusätzliche Abdrift
WW – Windwinkel (rwK – WR) WA - wind angle
WE – Windeinfallswinkel (rwSK – WR) RWA - relative wind angle
Steuerkurse heading
rwSK - Rechtweisender Steuerkurs TH - true heading
mwSK - Missweisender Steuerkurs MH - magnetic heading
KSK - Kompass Steuerkurs CH - compass heading
Kurse über Grund track
rwKüG - rechtweisender Kurs über Grund TT - true track
mwKüG - missweisender Kurs über Grund MT - magnetic track (nicht gebräuchlich)
9.1.4 Höhenmessereinstellungen
Vorwort
Der Höhenmesser ist eines der wichtigsten Instrumente im Flugzeug und wird daher auch in folgenden Fächern mit behandelt.
Kapitel 1.6 Flugnavigation und Luftfahrzeugbetrieb - 1.6.3 Flughöhe und Höhenmessereinstellungen
Kapitel 4.1 Begriffsbestimmungen – 4.1 Begriffe zu Höhe und Höhenmesser
Kapitel 8.6 Instrumentierung – 8.6.2 Mechanische Instrumente/ Druckinstrumente/Höhenmesser
Insofern können sich einige Inhalte wiederholen, enthalten jedoch dem Fach entsprechend wichtige Schwerpunkte, die du als Pilot kennen solltest.
In der praktischen Navigation ist es absolut notwendig die Begriffe QNH, QFE und QNE zu beherrschen.
Ein Höhenmesser arbeitet nach dem Prinzip eines Barometers. Er zeigt dir die Höhe bezogen auf eine Luftdruckfläche an. Je höher du fliegst, desto höher wird natürlich auch die angezeigte Flughöhe.
In der Abbildung hier ist er auf einen Druck von 1035hPa eingestellt auf den er sich bezieht. Der eingestellte Wert entspricht der Höhe über dem Meeresspiegel.
Eine detaillierte Beschreibung der Funktionsweise des Höhenmessers solltest Du im Technik Kapitel 8.6.2.2 nachlesen.
Abb. 9.1.4.1 Höhenmesser
In der Abbildung siehst du unten links am Instrument einen Drehknopf.
Mit ihm kannst du den eingestellten Luftdruck ändern und auf einen der folgenden Bezugsdrücke einstellen:
1. Druck auf Flugplatzniveau
2. Druck auf Niveau des Meeresspiegels
3. Druck der Standardatmosphäre (1013,2 hPa)
Für die Höhenmessereinstellung sind in Europa die folgenden drei Q-Codes relevant:
9.1.4.1 QFE bezeichnet die Höhe über Flugplatzniveau
Der QFE-Wert bezieht sich auf den in Flugplatzhöhe gemessenen Luftdruck. Ist der Höhenmesser so eingestellt, zeigt er die Höhe über dem Flugplatz an.
Um den Höhenmesser auf QFE einzustellen stellst du über den Drehknopf die beiden Zeiger am Boden auf Null.
Das ist bei der Landung natürlich praktisch, da dir die Höhe über deinem Flugplatz direkt angezeigt wird und du nicht rechnen musst. Bei einem kurzen Flug am Platz zeigt der Höhenmesser nach der Landung dann wieder auf Null.
Diese Einstellung wird aber nur bei lokalen Flügen um den Platz oder auch beim Kunstflug verwendet, wo es darauf ankommt die Höhe über dem Boden schnell erfassen zu können. In deiner Ausbildung wird i.d.R: aber bereits von Beginn an die im Folgenden erklärte Einstellung QNH verwendet. Mit ihr bist du in Bezug auf die dich umgebende Landschaft mit ihren Hindernissen sowie die möglicherweise in der Nähe befindlichen Lufträume stets auf der sicheren Seite.
Für Überlandflüge darf die QFE-Einstellung nicht verwendet werden! Hier ändert sich ja ständig die Geländehöhe während deines Fluges.
9.1.4.2 QNH bezeichnet die barometrische Höhe über Meeresniveau
Wird der Höhenmesser auf das QNH eingestellt so ist der Luftdruck auf Meereshöhe der Bezug.
Er zeigt somit auf dem Flugplatz am Boden dessen Höhe über dem Meeresspiegel an.
Für diese Einstellung fragst du entweder die Flugsicherung bzw. den Turm nach dem aktuellen Luftdruck am Platz oder du stellst einfach die bekannte Höhe des Flugplatzes über dem Meeresspiegel ein.
Diese Einstellung die überwiegend verwendete da sich alle Höhenangaben des Geländes auf unserer Luftfahrtkarte und auch viele Lufträume auf den Meeresspiegel beziehen. Bei Überlandflügen ist man oft viele Stunden in der Luft und fliegt in unterschiedlichen Gebieten. Das aktuelle QNH kann und wird sich daher wahrscheinlich ändern. Es ist daher sinnvoll bei FIS oder dem nächsten kontrollierten Flugplatz das aktuelle QNH zu erfragen und einzustellen, alternativ bietet sich an auch die ATIS des nächsten Flugplatzes abzuhören, hier erhält man auch das aktuelle QNH.
9.1.4.3 QNE bezeichnet die Standard-Höhenmessereinstellung (1013,2 hPa)
Auf internationaler Ebene hat man sich darauf verständigt, dass Flugzeuge ab einer bestimmten Höhe alle ihren Höhenmesser auf die gleiche Einstellung, das QNE, die sogenannte Standard-Höhenmessereinstellung, einstellen.
Beim QNE wird der Höhenmesser dann auf den festen Luftdruckwert 1013 hPa (Durchschnittswert der ICAO-Standardatmosphäre auf Meereshöhe) eingestellt.
Diese Einstellung ist besonders in der kommerziellen Luftfahrt aber auch bei VFR Motorflügen von Bedeutung. Hier herrscht wetterabhängig an den verschiedenen Flugplätzen oft ein unterschiedlicher lokaler Druck (QNH). So hat jedes Flugzeug beim Start zunächst eine andere Bezugsdruckfläche eingestellt und somit eine unterschiedliche Höhenanzeige. Daher ist es für die Sicherheit wichtig, dass all diese Flugzeuge mit der gleichen Einstellung also dem gleichen Bezug fliegen, damit es zu keinen Kollisionen in der Luft kommt.
Generell ab einer Flughöhe von 5000ft MSL bzw. 2000ft AGL, bzw. gemäß den beim Start an einem kontrollierten Flugplatz vorgegebenen Transition Level, wird der Höhenmesser daher auf QNE umgestellt und die Höhenangaben als Flightlevel oder Flugfläche bezeichnet.
Die Flugfläche wird hier in 100 ft Schritten angegeben. Die letzten beiden Nullen werden weggelassen. FL45 entspricht daher 4500 ft.
Abb. 9.1.4.3 Transition Level
Die Angabe (FL) findet sich bei vielen Lufträumen in unserer Luftfahrtkarte, typischerweise den Lufträumen Charlie, vereinzelt aber auch Delta. Du fragst dich jetzt sicherlich, wie wir das denn in unserem Segelflugzeug umsetzen sollen. Schließlich geht es in der Regel hier ständig auf und ab und es fällt uns daher schwer eine bestimmte Höhe einzuhalten. Somit scheint die QNE-Einstellung für uns eher weniger mit Sicherheit zu tun, ist es doch meist wichtiger den korrekten Bezug der Höhe zum Gelände, also das QNH, zu haben. Das ist zunächst richtig, jedoch kommt es durchaus häufig vor, dass wir uns an einem guten Tag auch über den 5000ft MSL bzw. 2000ft AGL bewegen, insbesondere bei Überlandflügen. Besonders im Nahbereich der größeren Flughäfen gibt es Lufträume deren Untergrenzen in FL angegeben sind und in die man ohne Freigabe nicht einfliegen darf. Sie dienen zum Schutz sowohl des an- und abfliegenden IFR Verkehrs als auch uns selbst (VFR Verkehr). Sobald ich mich in der Nähe der Untergrenze eines derartigen Luftraums bewege muss ich also wissen wie hoch ich in Bezug auf den (FL) bin und daher rechtzeitig den Höhenmesser auf QNE stellen.
Glücklicherweise verfügen heutzutage die meisten modernen Segelflugrechner über eine Funktionalität die dir auch die aktuelle Höhe als Flugfläche anzeigen, zudem können sie dich auch optisch und/oder akustisch warnen bevor du in einen gesperrten Luftraum einfliegst.
9.1.5 Maßeinheiten
In der Luftfahrt haben sich im Laufe der Zeit verschiedene Maßeinheiten aus dem Anglo Amerikanischen- als auch dem Metrischen System etabliert. Viele dieser Einheiten werden auch gemischt verwendet, sind leider nicht direkt umrechenbar was im Flug durchaus zu Problemen führen kann.
9.1.5.1 Längenmaße (Entfernungen)
Wie wir im Kapitel Koordinatensystem bereits besprochen haben gibt es die Maßeinheit Nautische Meile (NM).
Die Nautische Meile leitet sich ab aus einer Bogenminute und entspricht dem Erdumfang von 21600 NM geteilt durch 360° geteilt durch 60‘. Ein anderes Wort hierfür ist auch die Seemeile. Sie ist der Internationale Standard in der Luftfahrt!
In Deutschland hat sich allerdings schon sehr früh das Metrische System etabliert und findet Verwendung bei Entfernungen (Meter oder Kilometer). In Deutschland wird speziell beim Segelflug der Kilometer verwendet.
Sichtangeben erfolgen in Meter bzw. ab 5000 Meter in Kilometer.
1 NM entspricht 1852 Meter oder 1,852 Kilometer
Faustformel: NM = km / 2 + 10% Km = NM * 2 – 10%
Ein weiteres Längenmaß ist die englische Meile (auch Statute Mile). Eine englische Meile entspricht 1609 Meter. Dieses Maß ist in der Luftfahrt nicht gebräuchlich.
Das nächste wichtige Längenmaß ist das Fuß (ft) welches für Höhenangaben international Verwendung findet.
In Deutschland wird hier beim Segelflug standardmäßig meist der Meter verwendet.
1 ft entspricht 0,3048 m.
9.1.5.2 Geschwindigkeiten
Analog zu den Entfernungen gibt es daher bei den Geschwindigkeiten auch verschiedene Maßeinheiten.
Horizontale Geschwindigkeiten
Kilometer/Stunde (Km/h)
Nautische Meile/Stunde = Knoten (kt)
Die Faustformel zur Umrechnung entspricht der Faustformel die Entfernungen km – NM
Vertikale Geschwindigkeiten (Steig oder Sinkgeschwindigkeit)
Hier wird international die Einheit ft/min verwendet, dagegen hat sich im Segelflug in Deutschland m/s etabliert, international wird im Segelflug auch oft die Einheit kt verwendet.
Die Verwendung von Ft/min hat einen bestechenden Vorteil, lässt sich doch sehr einfach der Höhengewinn pro Minute errechnen, dies geht bei m/s deutlich schwieriger.
9.1.5.3 Druck
Der Luftdruck wird in hPa angegeben. Der Standard Luftdruck beträgt bekanntermaßen 1013,2 hPa.
In Amerika findet sich hier oft noch die Angabe in/hg (Zoll Quecksilbersäule). 29,92 in/hg entspricht dem Standard Luftdruck und wird oft als Druckangabe bei Constant Speed Propellerflugzeugen zur Leistungsangabe benutzt.
9.1.5.4 Wichtig
Als Pilot muss man jederzeit in der Lage sein mittels Faustformel km in Meter, km/h in Kt, ft in Meter und ft/min in m/s umzurechnen.
Die entsprechenden Formeln müssen daher auswendig gelernt werden.